Capítulo 7 Elementos de estatística básica no R

7.1 Parte 1

Assista este conteúdo em Cap 6 - Parte 1 no PVANet

Sempre que nos apoderamos de uma banco de dados antes de qualquer coisa precisamos entender o que eles guardam. Precisamos explorá-los e tentar extrair informações que possam representar os padrões ou ausência de padrões ou a variância dentro destes bancos de dados.

Vários métodos podem ser utilizados para extrair informações de um banco de dados. Podemos começar métodos mais simples e ir aumentando a complexidade a medida que vamos aprofundando nosso conhecimento sobre nosso banco de dados.
Para tirar conclusões ou fazer inferências precisaremos ir além dos métodos de descrição dos dados. No entanto, vamos inicialmente lançar mão em métodos de estatístrica descritiva. Como fazer isso no R?

7.1.1 Estatística Descritiva

De acordo com Mello and Peternelli (2013) estatística descritiva, como o próprio nome sugere, descreve e avalia certo grupo de dados, seja ele população ou amostra. Os autores ainda argumentam que temo na estatística descritva temos o método numérico e o método gráfico.

Vamos da uma olhada nos dados de consumo de cigarro nos Estados Unidos por ano.

Do jeito que a tabela está apresentada, ela pouco nos informa a respeito do comportamento dos dados. Mal podemos vê-la por completo deixando qualquer tentativa de sumarizar informações bastante frustrante.

Cons.Ciga<-read.csv("https://vincentarelbundock.github.io/Rdatasets/csv/Ecdat/Cigar.csv", header = T, row.names = 1)
str(Cons.Ciga)

## 'data.frame':    1380 obs. of  9 variables:
##  $ state: int  1 1 1 1 1 1 1 1 1 1 ...
##  $ year : int  63 64 65 66 67 68 69 70 71 72 ...
##  $ price: num  28.6 29.8 29.8 31.5 31.6 35.6 36.6 39.6 42.7 42.3 ...
##  $ pop  : num  3383 3431 3486 3524 3533 ...
##  $ pop16: num  2236 2277 2328 2370 2394 ...
##  $ cpi  : num  30.6 31 31.5 32.4 33.4 34.8 36.7 38.8 40.5 41.8 ...
##  $ ndi  : num  1558 1684 1810 1915 2024 ...
##  $ sales: num  93.9 95.4 98.5 96.4 95.5 ...
##  $ pimin: num  26.1 27.5 28.9 29.5 29.6 32 32.8 34.3 35.8 37.4 ...

library(rmarkdown)
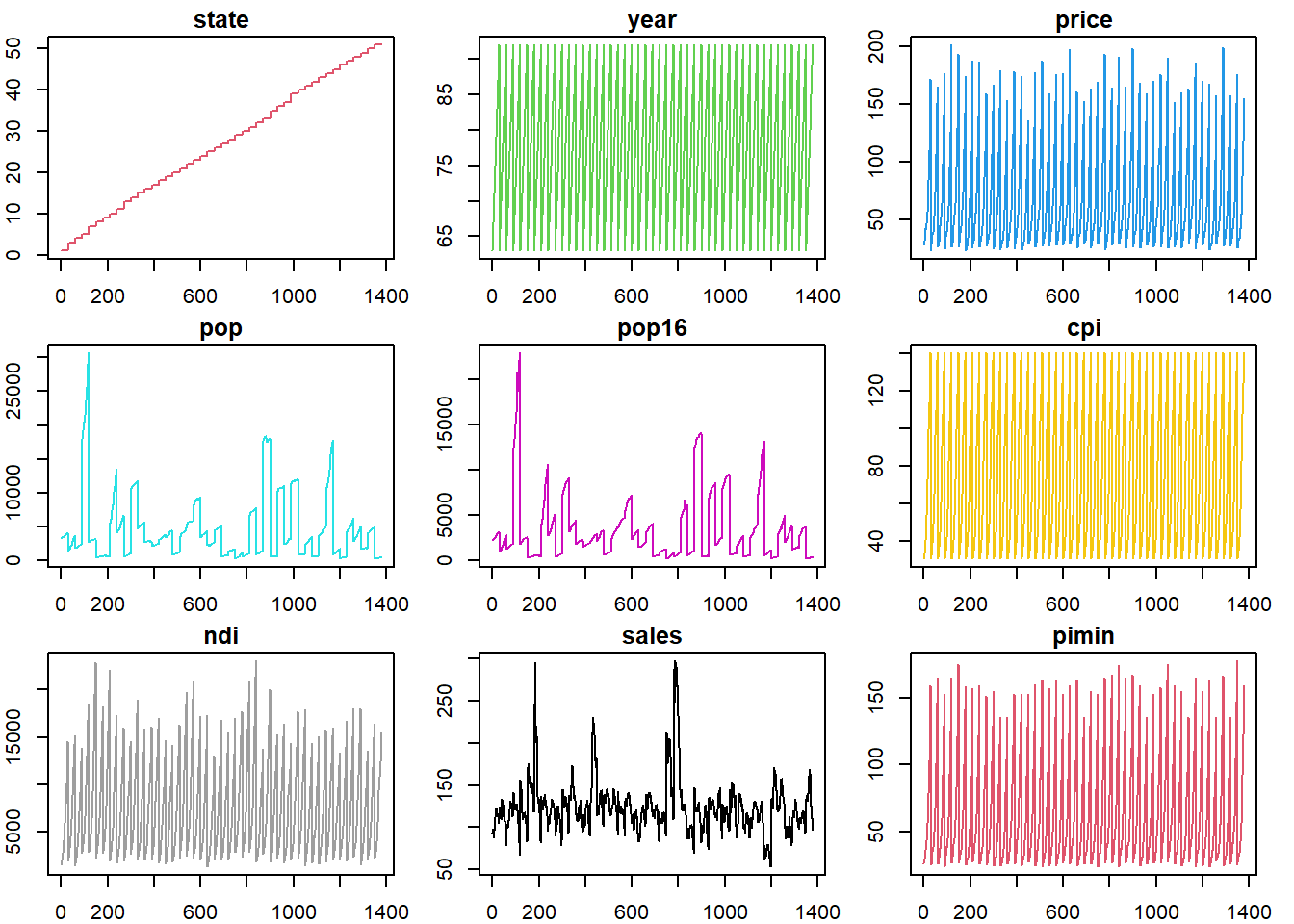
paged_table(Cons.Ciga)

Se tentarmos graficamente já dá uma melhorada, mas ainda não atender todas as expectativas.

par(mfrow=c(3,3), mar=c(2,2,1.5,1.5))
for(i in 1:ncol(Cons.Ciga)){
  plot(Cons.Ciga[,i], col=i+1, type="l", main=colnames(Cons.Ciga[i]))
 }

No entanto podemos começar buscando métodos “simples” de retirar informações.

7.1.1.1 Medidas de tendência central

7.1.1.1.1 Média

A média das observações é a famosa soma dos valores dividido pelo número de observações.

A função mean() calcula média de um vector. Caso queira médias por variáveis ou observações você pode utilizar colMeans().

(20+31+54+78+12)/5

## [1] 39

mean(c(20,31,54,78,12))

## [1] 39

mean(Cons.Ciga$price)

## [1] 68.69993

colMeans(Cons.Ciga)

##      state       year      price        pop      pop16        cpi        ndi 
##   26.82609   77.50000   68.69993 4537.11319 3366.61609   73.59667 7525.02302 
##      sales      pimin 
##  123.95087   62.89928

media.linhas<-as.matrix(rowMeans(Cons.Ciga))

plot(media.linhas, type="l")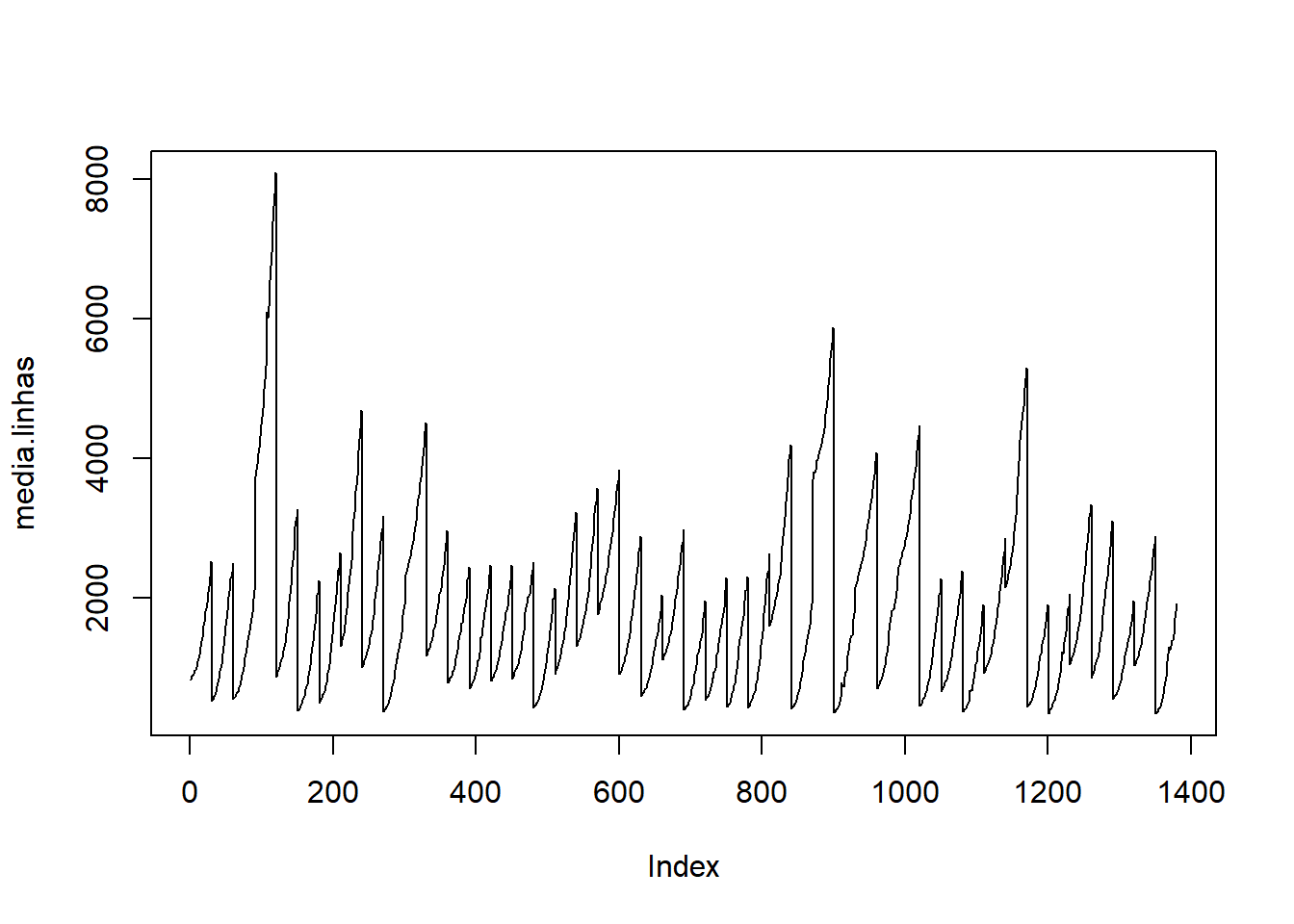

paged_table(as.data.frame(media.linhas))

Se você quiser apenas a soma use sum(), rowSums e colSums().

(20+31+54+78+12)

## [1] 195

sum(c(20,31,54,78,12))

## [1] 195

sum(Cons.Ciga$price)

## [1] 94805.9

colSums(Cons.Ciga)

##      state       year      price        pop      pop16        cpi        ndi 
##    37020.0   106950.0    94805.9  6261216.2  4645930.2   101563.4 10384531.8 
##      sales      pimin 
##   171052.2    86801.0

Soma.linhas<-as.matrix(rowSums(Cons.Ciga))

plot(Soma.linhas, type="l")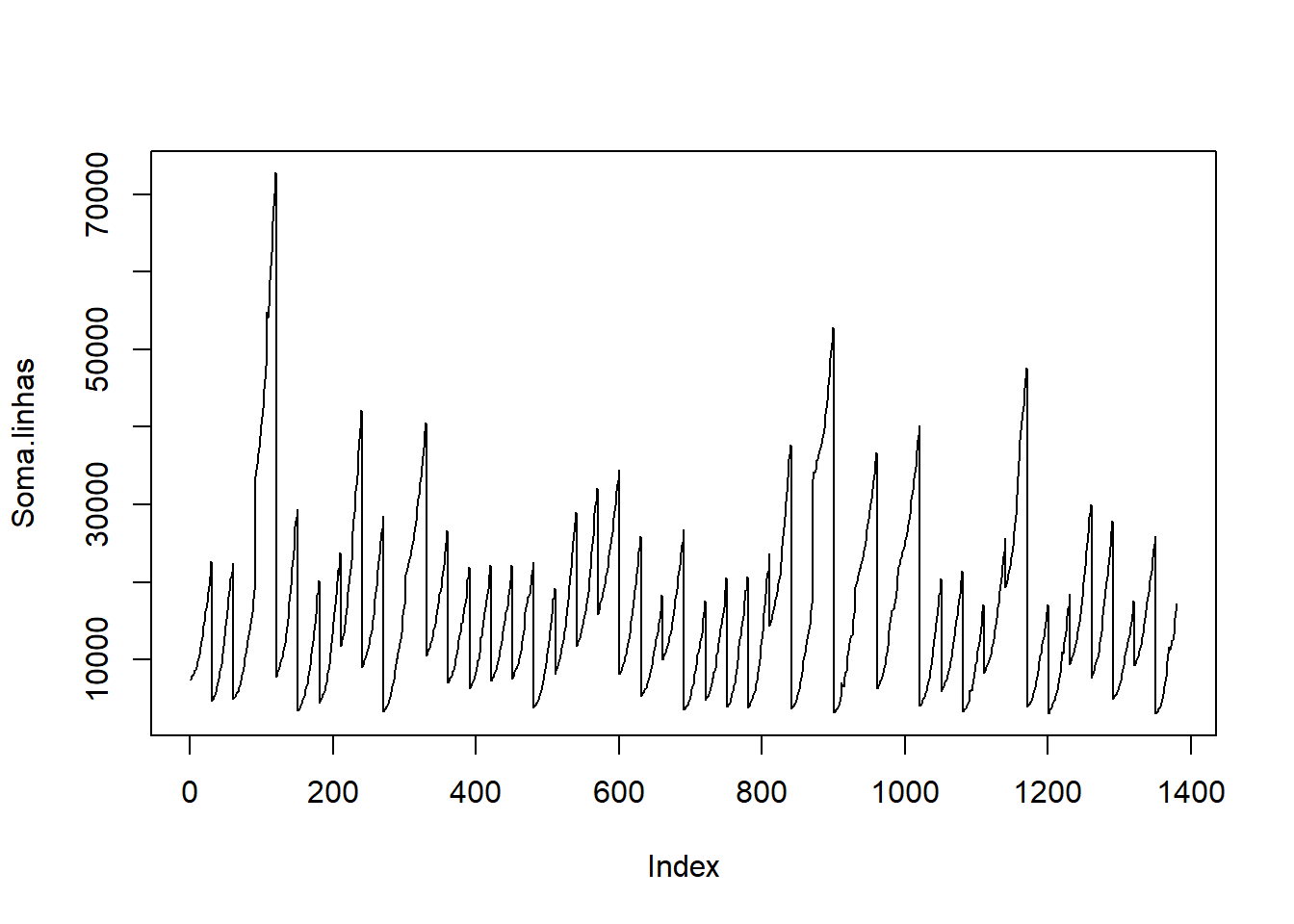

paged_table(as.data.frame(Soma.linhas))

7.1.1.1.2 Média Aparada

No mundo real, em dados observados, muitas vezes encontramos dados que fogem do padrão dos outros elementos.
Imagine que você coletou um banco de dados com os seguintes valores.

-435, 34, 20, 18, 33, 26, 27, 29, 31, 19

Há algo de estranho com esse -435. Ele provavelmente é um outlier, um valor que foi de maneira equivocada coletado por falha do pesquisador ou falha no equipamento.

De acordo com Navarro (2013) quando encaramos esse tipo de condição com valores extremos no meio de nossos dados, uma média aritmética não é o método mais indicado, pois ela sofre muita influêncioa dos valores extremos.

Para casos como esses podemos calcular uma mediana ou uma média aparada. Para calcular uma média aparada vamos descartar os valores extremos preservando os valores “reais” ou “corretos” de nossas observações. Tendo as características preservadas em nosso banco de dados poderemos então partir para análises mais sofisticadas.

A média aparada é descrita em termos de porcentagem de observações. Por exemplo, uma média aparada em 10% descarta os 10% dos dados maiores e os 10% menores calculando assim a média aritmética dos 80% restantes.

Para calcular a média aparada no R utilize o argumento trim=x (x é uma valor que vai de 0.0 (0%) até 1 (100%)) dentro com comando mean().

set.seed(1234)
temp<-c(-100,runif(n=10, min = 20, max = 38))
temp

##  [1] -100.00000   22.04666   31.20139   30.96695   31.22083   35.49648
##  [7]   31.52559   20.17092   24.18591   31.98951   29.25652

mean(temp)

## [1] 17.09643

mean(temp, trim=0.0)

## [1] 17.09643

mean(temp, trim=0.1)

## [1] 28.0627

7.1.1.1.3 Mediana

Medida utilizada para indicar o centro de um conjunto de dados ou o valor intermediário.
Se n for ímpar a posição da mediana será (n+1)/2.

Em 9, 25, 36, 49, 49 a mediana é 36.

Se n for par, a mediana será a média aritmética dos valores que ocupam as posições n/2 e n/2+1.
Em 9, 25, 35, 36, 49, 49 a mediana é 35.5.

A mediana é uma medida útil quando temos valores extremos discrepantes dos demais (Mello and Peternelli (2013)). No R pode ser alcançada utilizando o comando median().

median(c(9, 25, 36, 49, 49))

## [1] 36

median(c(9, 25, 35, 36, 49, 49))

## [1] 35.5

for(i in 1:ncol(Cons.Ciga)){
  print(noquote(paste(c('Mediana de', colnames(Cons.Ciga[i]), 'é', round(median(Cons.Ciga[,i]),digits=2)))))
}

## [1] Mediana de state      é          26.5      
## [1] Mediana de year       é          77.5      
## [1] Mediana de price      é          52.3      
## [1] Mediana de pop        é          3174      
## [1] Mediana de pop16      é          2315.3    
## [1] Mediana de cpi        é          62.9      
## [1] Mediana de ndi        é          6281.2    
## [1] Mediana de sales      é          121.2     
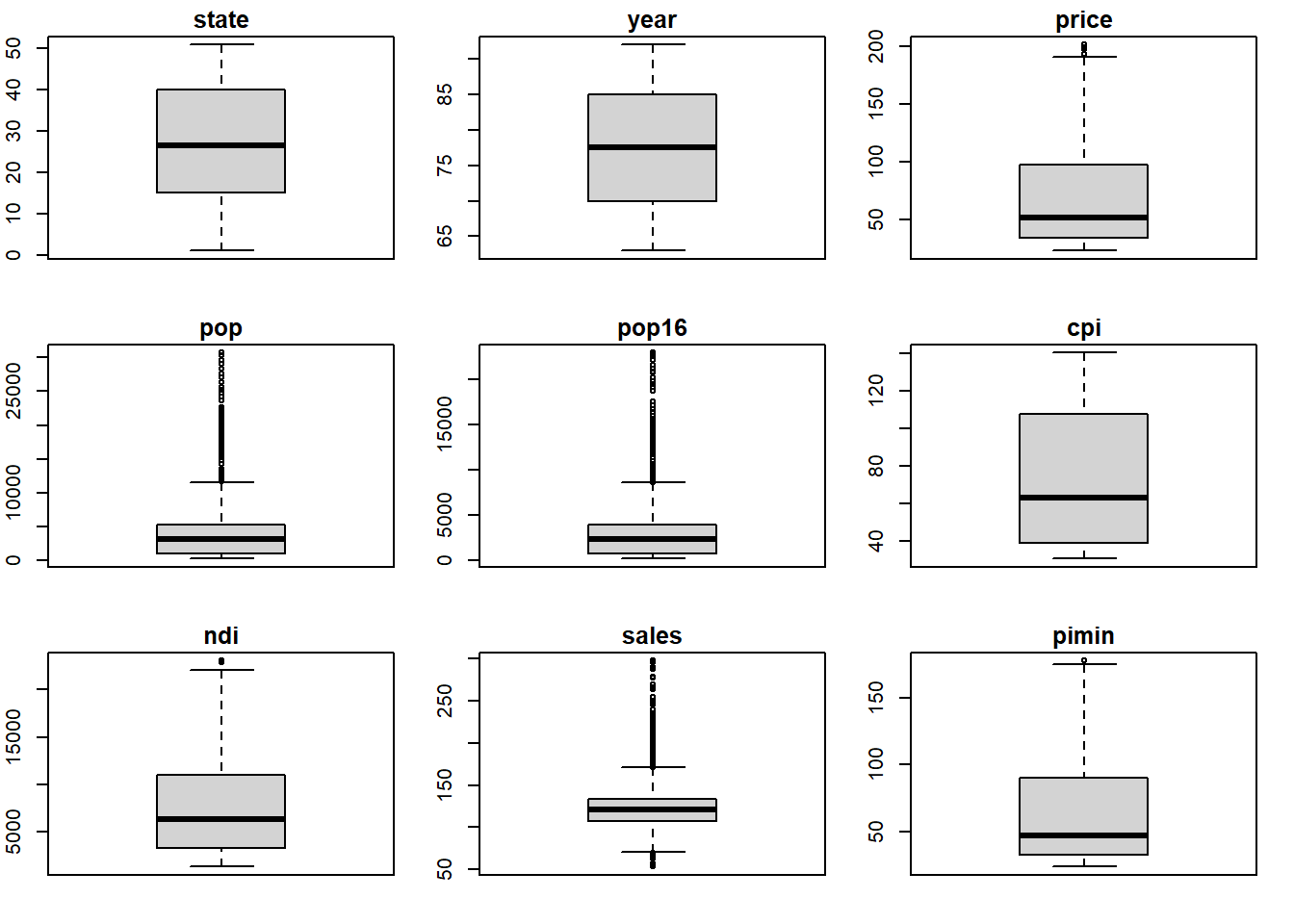
## [1] Mediana de pimin      é          46.4

par(mfrow=c(3,3),mar=c(2,2,1.5,1.5))
for(i in 1:ncol(Cons.Ciga)){
  (boxplot(Cons.Ciga[,i], main=colnames(Cons.Ciga[i])))
  }

7.1.1.1.4 Moda

Um conjunto de dados pode ser unimodal, bimodal ou amodal. A moda pode ser usada para indicar tendência central de um conjunto de observações (moda amostral).

No R podemos calcular a moda pela utilização da função mfv() ou mfv1() de alguns pacotes como modeest ou criar uma função para isso uma vez que não conhecemos uma função nativa que calcule a moda.

#install.packages("modeest")
library(modeest)

## Registered S3 method overwritten by 'rmutil':
##   method         from
##   print.response httr

# Atenção, pois `mfv()` e `mfv1()`produzem resultados diferentes.

for(i in 1:ncol(Cons.Ciga)){
  print(noquote(paste(c('A moda de', colnames(Cons.Ciga[i]), 'é', round(mfv1(Cons.Ciga[,i]),digits=2)))))
}

## [1] A moda de state     é         1        
## [1] A moda de year      é         63       
## [1] A moda de price     é         30.1     
## [1] A moda de pop       é         703      
## [1] A moda de pop16     é         523.3    
## [1] A moda de cpi       é         30.6     
## [1] A moda de ndi       é         13318    
## [1] A moda de sales     é         122.3    
## [1] A moda de pimin     é         30.1

#Criando a própria função para MODA
moda <- function(v) {
   uniqv <- unique(v)
   uniqv[which.max(tabulate(match(v, uniqv)))]
   }

for(i in 1:ncol(Cons.Ciga)){
  print(noquote(paste(c('A moda de', colnames(Cons.Ciga[i]), 'é', round(moda(Cons.Ciga[,i]),digits=2)))))
}

## [1] A moda de state     é         1        
## [1] A moda de year      é         63       
## [1] A moda de price     é         30.1     
## [1] A moda de pop       é         703      
## [1] A moda de pop16     é         559.3    
## [1] A moda de cpi       é         30.6     
## [1] A moda de ndi       é         13318    
## [1] A moda de sales     é         122.3    
## [1] A moda de pimin     é         30.1

Temos também a função maxFreq()que retorna a frequência modal.

#install.packages("lsr")
library(lsr)

seleções.campeãs<-as.factor(c("Uruguai","Itália","Itália","Sem Copa","Sem Copa","Uruguai","Alemanha","Brasil",
           "Brasil","Inglaterra","Brasil","Alemanha","Argentina","Itália","Argentina",
           "Alemanha","Brasil","França","Brasil","Itália","Espanha","Alemanha","França"))

table(seleções.campeãs)

## seleções.campeãs
##   Alemanha  Argentina     Brasil    Espanha     França Inglaterra     Itália 
##          4          2          5          1          2          1          4 
##   Sem Copa    Uruguai 
##          2          2

modeOf(seleções.campeãs) # Mostra a moda (aquele que mais se repete)

## [1] "Brasil"

maxFreq(seleções.campeãs) # Mostra a frequência daquele que mais se repete

## [1] 5

7.1.1.2 Medidas de Variabilidade

7.1.1.2.1 Amplitude

É simplesmente a diferença entre o maior e menor valor dentro de um conjunto de dados. Podemos utilizar os comandos max() e min() para acessar os valores máximos e mínimos do conjunto de dados ou range() que mostra os dois valores (máximo e mínimo) ao mesmo tempo.

max(Cons.Ciga$price)-min(Cons.Ciga$price)

## [1] 178.5

range(Cons.Ciga$price)

## [1]  23.4 201.9

range(Cons.Ciga$price)[2]

## [1] 201.9

range(Cons.Ciga$price)[1]

## [1] 23.4

range(Cons.Ciga$price)[2]-range(Cons.Ciga$price)[1]

## [1] 178.5

for(i in 1:ncol(Cons.Ciga)){
  print(noquote(paste(c('A Amplitude de', colnames(Cons.Ciga[i]), 'é', round(max(Cons.Ciga[,i])-min(Cons.Ciga$price),digits=2)))))
}

## [1] A Amplitude de state          é              27.6          
## [1] A Amplitude de year           é              68.6          
## [1] A Amplitude de price          é              178.5         
## [1] A Amplitude de pop            é              30679.9       
## [1] A Amplitude de pop16          é              22896.6       
## [1] A Amplitude de cpi            é              116.9         
## [1] A Amplitude de ndi            é              23050.6       
## [1] A Amplitude de sales          é              274.5         
## [1] A Amplitude de pimin          é              155.1

7.1.1.2.2 Classificação percentil

A classificação percentil de um dado qualquer define a porcentagem dos casos em uma distribuição que se enquandram naquele valor ou abaixo dele.
Imagine que temos as seguintes notas de um conjunto de alunos e queremos saber quantas notas ficaram dentro de 60% total das notas. Podemos proceder com classificação percentil utilizando quantile(x=, probs = ).

94, 92, 91, 88, 85, 84, 80, 79, 77, 76, 74, 74, 71, 69, 65, 62, 56, 53, 48, 40

notas<-c(94, 92, 91, 88, 85, 84, 80, 79, 77, 76, 74, 74, 71, 69, 65, 62, 56, 53, 48, 40)

quantile(x = notas, probs = .60)

##  60% 
## 77.8

quantile( x = Cons.Ciga$price, probs = .50)

##  50% 
## 52.3

print(noquote(paste(c('Observamos que 50% das estão abaixo de',(quantile(x = Cons.Ciga$price, probs = .50)[[1]]),"."))))

## [1] Observamos que 50% das estão abaixo de
## [2] 52.3                                  
## [3] .

7.1.1.2.3 Variação interquartil

A variação interquartil (IQR - Interquartile range) mede a amplitude entre os quartis 1 (contém 25% dos dados) e 3 (contém 75% dos dados).

quantile( x = Cons.Ciga$price, probs = .25)

##    25% 
## 34.775

quantile( x = Cons.Ciga$price, probs = .75)

##  75% 
## 98.1

quantile( x = Cons.Ciga$price, probs = c(0.25,0.75))

##    25%    75% 
## 34.775 98.100

library(mosaic)

## Registered S3 method overwritten by 'mosaic':
##   method                           from   
##   fortify.SpatialPolygonsDataFrame ggplot2

## 
## The 'mosaic' package masks several functions from core packages in order to add 
## additional features.  The original behavior of these functions should not be affected by this.

## 
## Attaching package: 'mosaic'

## The following object is masked from 'package:Matrix':
## 
##     mean

## The following objects are masked from 'package:dplyr':
## 
##     count, do, tally

## The following objects are masked from 'package:analogue':
## 
##     compare, mat

## The following object is masked from 'package:permute':
## 
##     shuffle

## The following object is masked from 'package:purrr':
## 
##     cross

## The following object is masked from 'package:ggplot2':
## 
##     stat

## The following objects are masked from 'package:stats':
## 
##     binom.test, cor, cor.test, cov, fivenum, IQR, median, prop.test,
##     quantile, sd, t.test, var

## The following objects are masked from 'package:base':
## 
##     max, mean, min, prod, range, sample, sum

IQR(x = Cons.Ciga$price )

## [1] 63.325

par(mar=c(0.5, 4, 0.2, 0.2), mfrow=c(2,1),
     oma = c(4, 4, 0.2, 0.2))

boxplot(Cons.Ciga$price, ylim=c(min(0), max(Cons.Ciga$price)),
xlab = "",ylab = "",col = "orange",xaxt='n',
yaxt="n",border = "brown",horizontal = TRUE,notch = TRUE)

quant<-quantile(Cons.Ciga$price,probs = c(0.25,0.5,0.75))

plot.ecdf(Cons.Ciga$price, pch = 1, xlim=c(min(0), max(Cons.Ciga$price)), col="orange", main="",ylab="", xlab="")

mtext(text = "Preço do cigarro",side = 1,line = 2)
mtext(text = "Frequência relativa acumulada",side = 2,line = 2)

segments(-10,0.25,quant[[1]],0.25, col="blue",lwd=2)
arrows(quant[[1]],0.25,quant[[1]],0, col="blue",lwd=2)
text(x = -5, y = 0.30, paste0("Q1 = ",quant[[1]]), 
     cex = 0.8, col = "blue", family="mono", font=2, adj=0)

segments(-10,0.5,quant[[2]],0.5, col="darkviolet",lwd=2)
arrows(quant[[2]],0.5,quant[[2]],0, col="darkviolet",lwd=2)
text(x = -5, y = 0.60, paste("Q2 ou \nMediana = ",quant[[2]]), 
     cex = 0.8, col = "darkviolet", family="mono", font=2, adj=0)

segments(-10,0.75,quant[[3]],0.75, col="red",lwd=2)
arrows(quant[[3]],0.75,quant[[3]],0, col="red",lwd=2)
text(x = -5, y = 0.8, paste("Q3 = ",quant[[3]]), 
     cex = 0.8, col = "red", family="mono", font=2, adj=0)

text(x = 150, y = 0.4, paste("Variação \nInterquartil \n(IQR) = ",IQR(Cons.Ciga$price)), cex = 1, col = "black", family="mono", font=2, adj=0.5)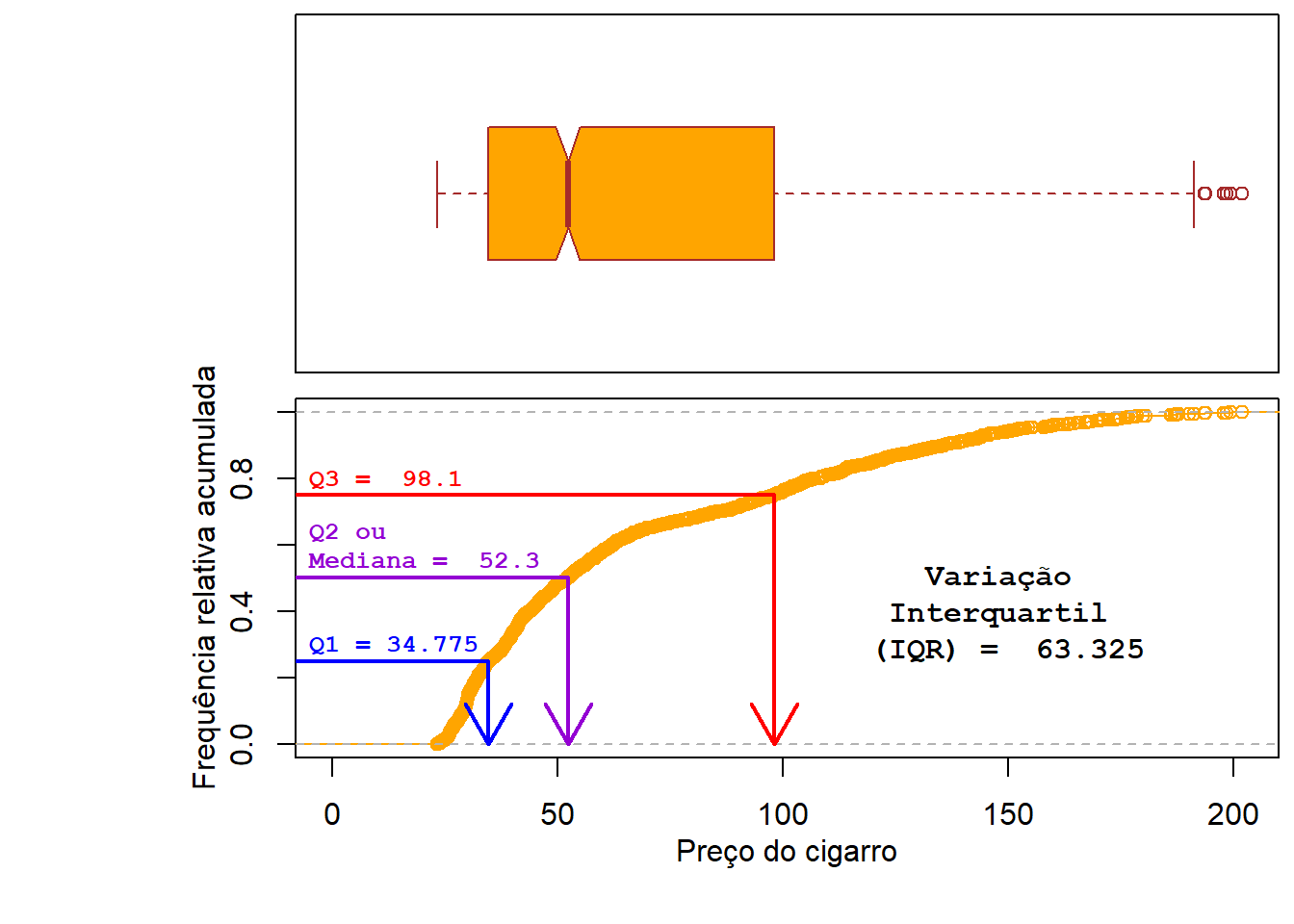

7.1.1.2.4 Desvios

Até o momento vimos 2 maneiras de medir a dispersão dos dados (amplitude e o variação interquartil).
Podemos, baseado em um valor de referência, avaliar a o desvio médio absoluto, que nada mais é do que o somatório das distâncias dos dados em relação à sua média ou mediana.

\[\begin{align} (X) = \frac{1}{N} \sum_{i = 1}^N |X_i - \bar{X}| \end{align}\]

Para ser honesto, eu nunca vi isso sendo utilizado como produto final, mas é um passo importante para entender seus dados e as próximas análises a serem desenvolvidas. De acordo com Navarro (2013) a o desvio com base na mediana é melhor que utilizando a média. Mas vamos dar uma olhada em ambas.

Primeiramente temos que definir nossa base por exemploe a média. Retornando para nosso exemplo de preços de cigarro temos que a média dos preços é 68.69993. Vamos dar uma olhada nos valores apenas no Quartil 1.

No R podemos fazer passo a passo ou utilizando o pacotelsr.

library(rmarkdown)
mean(Cons.Ciga$price)

## [1] 68.69993

Q1<-subset(Cons.Ciga,price<quant[[1]])
Q1.desv<-abs(Q1$price-(mean(Q1$price)))

Desvio<-as.data.frame(cbind(Q1$price,Q1.desv))

colnames(Desvio)<-c("X","X-Xmed")

paged_table((Desvio))

print(mean(Desvio$`X-Xmed`)) # Desvio absoluto médio

## [1] 2.290828

library(lsr)
aad(Desvio$X)

## [1] 2.290828

O desvio absoluto médio do primeiro quartil é 2.291. Isto mostra a média das distância entre cada dado do Quatil 1 e a média.

7.1.1.2.5 Variância

Diferentemente do desvio médio absoluto, a variância eleva a soma dos desvios ao quadrado.

\[\begin{align} \sigma^2 = \frac{\sum_{i=1}^{n}(x_i - \mu)^2} {n} \end{align}\]

No R podemos fazer passo a passo ou utilizando o comando var().

sum((Desvio$X-mean(Desvio$X))^2/(length(Desvio$X)-1))

## [1] 7.905433

var(Desvio$X)

## [1] 7.905433

7.1.1.2.6 Desvio Padrão

Quando elevamos os desvios ao quadrado criamos um problema, pois mudamos a unidade dos dados originais. Para colocar a medida de variabilidade na escala original, calculamos a raiz quadrada da variância e, com isso, temos o desvio padrão.

\[\begin{align} \hat\sigma = \sqrt{ \frac{1}{N-1} \sum_{i=1}^N \left( X_i - \bar{X} \right)^2 } \end{align}\]

Mesmo assim a interpretação do desvio padrão é um tanto complexa. Vamos pensar em termos de desviopadrão da média numa distribuição de normal. Quanto mais longe do média, maior o desvio padrão.
Como discutido exaustivamente na lista 1, esperamos que aproximadamente 68% dos valores de dados normalmente distribuídos fiquem entre -1 e +1 desvio padrão da média, aproximadamente 95% entre -2 e +2 e paroximadamente 99% entre -3 e +3.

Obviamente esta definição se aplica à dados perfeitamente encaixados na distribuição normal, mas no mundo real isso é um pouco mais complexo e quanto menor a amostra pior fica.

No R podemos calcular manualmente ou utilizando o comando sd().

Veja abaixo que a distribuição mesocúrtica dos nossos dados de preços de cigarro (linha azul), apenas do 1° quartil, se assemelha à distribuição normal “perfeita” (linha vermelha) principalemnte nos extremos possuindo e excetuando em aproximadamente -1 e + 1 desvio padrão.

sqrt(sum((Desvio$X-mean(Desvio$X))^2/(length(Desvio$X)-1)))

## [1] 2.81166

sd(Desvio$X)

## [1] 2.81166

library(tidyverse)

Desvio<-Desvio %>% 
  mutate(zscore = (Desvio$X - mean(Desvio$X))/sd(Desvio$X))

head(Desvio)

##      X     X-Xmed      zscore
## 1 28.6 1.18376812 -0.42102104
## 2 29.8 0.01623188  0.00577306
## 3 29.8 0.01623188  0.00577306
## 4 31.5 1.71623188  0.61039803
## 5 31.6 1.81623188  0.64596420
## 6 23.9 5.88376812 -2.09263124

plot(density(Desvio$zscore), frame = FALSE, col = "blue", xlim=c(-3,3),lwd=3, ylim=c(0,0.4),main = "Densidade do Quartil 1", type="l", xlab="", ylab="")
abline(v=mean(Desvio$zscore), col="blue", lwd=2,lty=4)

par(new=T)
x.values = seq(-3,3, length = 345)
y.values = dnorm(x.values)

plot(x.values, y.values, type="l", lty=1, xlab="", xlim=c(-3,3),ylim=c(0,0.4), ylab="",col="red")
abline(v=mean(x.values), col="red", lwd=2, lty=3)

abline(v=c(-1,1), col="grey", lwd=2, lty=4)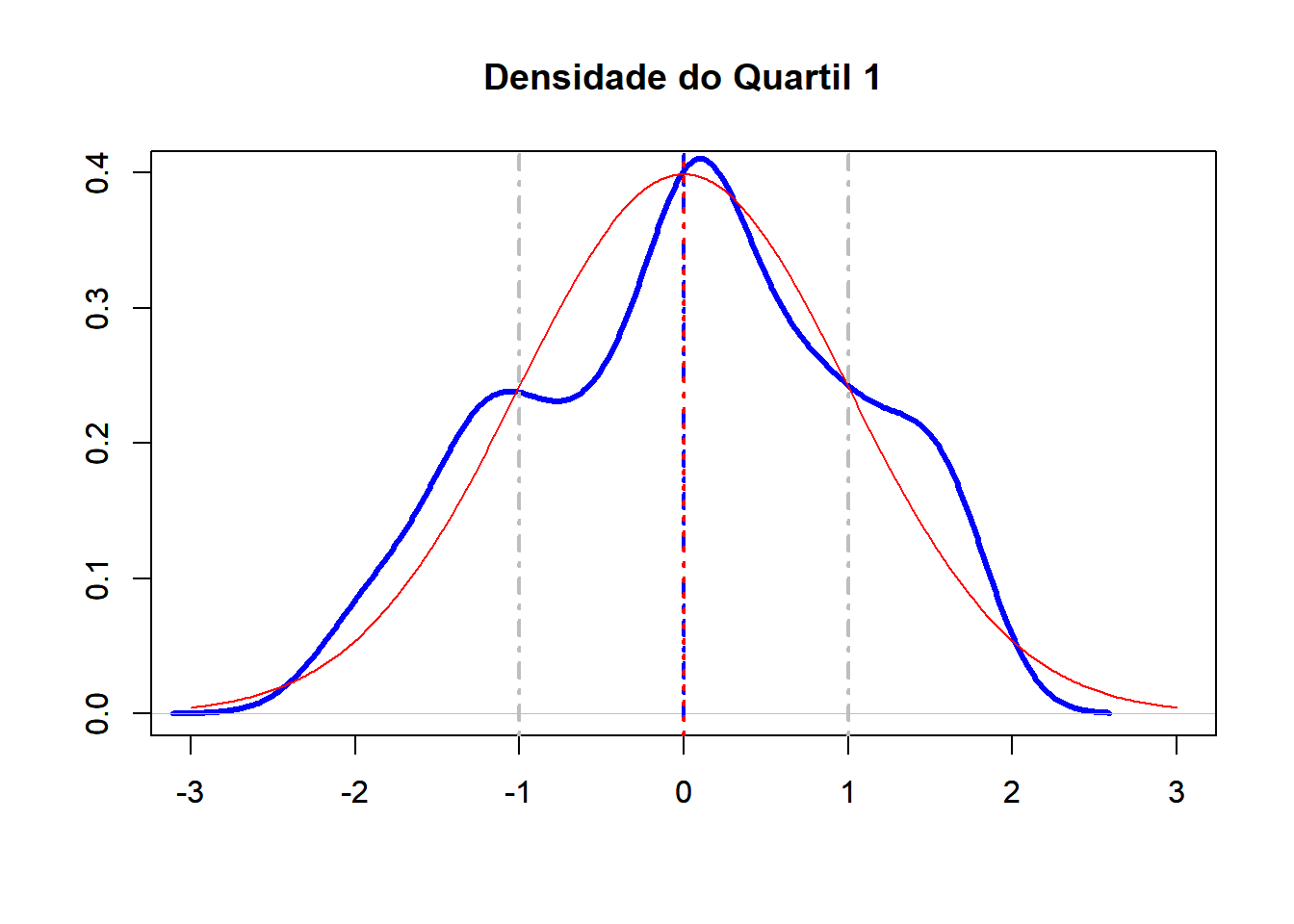

Desv.pad.68.perc<-(Desvio$zscore[(Desvio$zscore >= -1.0) & (Desvio$zscore <= 1.0)])
(length(Desv.pad.68.perc)/length(Desvio$zscore))*100

## [1] 61.44928

Veja que o preço dos cigarros do 1° quartil entre -1 e +1 desvio padrão ficam em 61.45%. Experimente fazer com toda a amostra.

Navarro (2013) faz um resumo interessante sobre quando utilizar cada um das medidas até discutidas.

Amplitude: Mostra a dispersão máxima dos dados. É sensível a valores extremos ou outliers sendo utilizada quando queremos avaliar a variação entre os extremos como no caso da temperatura na meteorologia.

Variação Interquartil: Excelente método de exploração de dados fornecendo um conjunto de informações de uma só vez principalemnte quando acompanhando de boxplot.

Desvio médio absoluto: Mostra quão distante da média as observações estão.

Variância: Descreve a variação dos dados ao redor da média com a limitação da dificuldade de interpretação em razão da escala ser diferente dos dados originais.

Desvio Padrão: É oe método mais utilizado para medida de variação dos dados. É dado pela raiz quadrada da variância sendo mais simples de interpretar que a variância uma vez que está na mesma unidade de medida que os dados originais.

7.1.2 Leituras complementares

Descriptive statistics in R

Yamamoto (2020)

Kabacoff (2015)

7.2 Parte 2

Assista este conteúdo em Cap 6 - Parte 2 no PVANet

7.2.1 Teste de diferença entre médias

Todos os trabalhos que conduzimos necessitam minimamente de algum teste estatístico. Seja ele descritivo, inferencial ou para testar hipóteses. Especificamente no ultimo caso, quando tratamos de experimentos precisamos conduzir testes para indentificar se nossa hipótese é plausível ou não (Mello and Peternelli (2013)).
Suponhamos que queremos comprar um fertilizante para nossa lavoura de milho, mas não sabemos se vale a pena. Para decidir qual é o melhor, podemos conduzir experimentos na produção de milho para testá-lo com objetivo de saber se há ganho na produtividade.

set.seed(1234)
exper<-runif(25, min = 4350, max = 4900)

Suponhamos que a produtividade média sem fertilizante seja 4.350 kg ha e com o uso do fertilizante foi 4580.47 kg ha.

Podemos dizer que o uso do fertilizante namédia aumentou a produtividade, mas será que vale a pena gastar mais para ter esse aumento? Talvez, talvez não. Não podemos tirar muitas conclusões baseados apenas nestas informações.

Poderíamos calcular, as médias (4580.47), a mediana (4516.48), a variância (2.12961^{4}) o desvio padrão (145.93) e todos os outro métodos de análise descritiva que vimos até agora, mas mesmo assim seria inapropriado tomar uma decisão sobre a compra do fertilizante baseando-nos apenas numa medida central. Uma maior segurança em nossa tomada de decisão seria balizada por uma comparação da eficiência do uso de fertilizante com o não uso.

Para realizar tal procedimento vamos seguir os passos sugeridos por Freire (2021a):

7.2.1.1 1 - Estabelecer um hipótese a ser testada

A hipótese a ser testada é a hipótese nula (\(H_0\)) e a hipótese que será confrontada será a hipótese de pesquisa é (\(H_1\)).

Na hipótese nula assumimos que as médias das amostras ou populações que estamos comparando são iguais e nossa hipótese de pesquisa diz que não são iguais.

\(H_0: \mu_A = 4.350\)

\(H_1: \mu_A \ne 4.350\)

7.2.1.2 2 - Decidir qual teste utilizar

A partir da hipótese nula podemos decidir qual teste será mais apropriado. No nosso exemplo poderíamos selecionar uma amostra de 25 espigas de milho de cada tratamento e compararmos as médias (kg) das amostras conforme estabelecido pela hipótese nula (\(H_0\)). Teremos assim um distribuição t de Student com n-1 graus de liberdade.

7.2.1.3 3 - Selecionar o nível de significância (\(\alpha\))

O nível de \(\alpha\) define a região crítica da distribuição. Com este valor vamos identificar se a diferença amostral é estatísticamente significativa - se é o resultado da diferença de população real, e não apenas um erro amostral. Se o valor da estatística calculada a partir da amostra selecionada cair na região crítica, a hipótese nula (\(H_0\)) será rejeitada e ficamos com a hipótese de pesquisa (\(H_1\)). Assumimos rejeitamos a hipótese nula se a probabilidade for muito pequena ( por exemplo, menos de 5 em 100), o que significqa que a diferença entre de amostra seria um produto do erro amostral. Caso contrário não a rejeitamos \(H_0\).
Normalmente os valores de \(\alpha\) são 0.1 (10%), 0.05 (5%) e 0.01 (1%).

Cuidado com o termo “aceitar \(H_0\)”. O correto é “não rejeitar \(H_0\)”.

Considerando que a estatística t, definida no passo 2, segue a distribuição t de Student na figura abaixo destacando as regiões críticas

Fonte: Freire (2021a)

Podemos definir nosso nível de significância em 10%, 5% e 1%. No R podemos calcular com a função qt

qt(0.95,24) #0.05 de cada lado

## [1] 1.710882

qt(0.975,24) #0.025 de cada lado

## [1] 2.063899

qt(0.995,24) #0.005 de cada lado

## [1] 2.79694

Desta forma termos nosso nível de significância para 10% igual 1.7108821, para 5% igual 2.0638986 e para 1% igual a 2.7969395.

Fonte: Levin, Fox, and Forde (2012)

7.2.1.4 4 - Selecionar a amostra, realizar os cálculos e tomar a decisão

Após os passos 1, 2 e 3 procedemos a seleção da amostra do estudo, a partir da qual o valor da estatística será calculado e comparado com os valores críticos. Caso o valor da estatística caia dentro da região crítica do teste, a hipótese nula será rejeitada. Neste caso, dizemos que o resultado do teste é estatisticamente significativo. Caso contrário, ela não será rejeitada e o resultado do teste não é estatisticamente significativo.

7.2.1.5 Tipos de erros inerentes ao testes de hipótese

Ao realizarmos os testes estamos sujeitos a comenter 2 tipos erros.

ERRO tipo 1: Rejeitar \(H_0\) quando \(H_0\) é verdadeira. Isto pode acontecer quando extraímos uma amostra da população e a estatística calculada a partir dessa amostra cai na região crítica. Ao fixarmos α, fixamos a probabilidade deste erro.

ERRO tipo 2: Não rejeitar \(H_0\) quando esta for falsa.Isto acontece quando extraímos uma amostra da população e a estatística calculada a partir dessa amostra cai na região crítica.

7.2.1.6 P-value (Valor P ou P valor)

Ao testar uma hipótese podemos a priori dcefinir o nível de significância \(\alpha\). O valor de \(\alpha\) se refere ao tamanho das regiões da extremidade sob a curva que nos levarão a rejeitar a hipótese nula. Ou seja, é a área à direita ou equerda do valor crítico.

O valor de P (P value) é a probabilidade exata de se obter dados de uma amostra quando a hipótese nula é verdadeira. Desta forma, o valor de \(\alpha\) é o limiar do qual a probabilidade é considerada tão pequena (P<\(\alpha\)) que decidimos rejeitar a hipótese nula.

options(scipen = 999)
t.test(exper)

## 
##  One Sample t-test
## 
## data:  exper
## t = 156.94, df = 24, p-value < 0.00000000000000022
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  4520.229 4640.704
## sample estimates:
## mean of x 
##  4580.466

Acima visualizamos o teste bilateral, mas temos também testes unilaterais.

Em outros cenários, o interesse pode ser em testar se o desvio em relação à hipótese nula ocorre em somente uma direção. Por exemplo, ao testar um medicamento para reduzir a pressão arterial de pacientes hipertensos, os investigadores estão interessados somente se ocorre uma redução da pressão arterial após o uso do medicamento testado. Se houver um aumento da pressão ou nenhuma alteração no valor da pressão arterial, então o medicamento será considerado ineficaz. Neste caso, sendo μ a variação média do valor da pressão arterial, a hipótese nula será \(\mu\ge0\) e a hipótese alternativa será \(\mu<0\), ou seja, a hipótese nula será rejeitada somente se a variação média da pressão arterial for menor que o valor crítico, determinado a partir do nível de significância (α) e da distribuição da estatística utilizada. Neste caso, o teste é chamado de teste unilateral (one-sided test). O valor de p será igual à probabilidade, sob a hipótese nula, de se observar um valor da estatística utilizada no teste de hipótese abaixo ou igual ao valor calculado na amostra utilizada no estudo.

Como outro exemplo de teste unilateral, agora na direção oposta, em um teste de um medicamento vasodilatador, os investigadores estão interessados somente se ocorre um aumento do diâmetro dos vasos sanguíneos após o uso do medicamento testado. Se houver uma redução ou nenhuma alteração no diâmetro dos vasos, então o medicamento será considerado ineficaz. Neste caso, sendo μ a variação média do valor do diâmetro do vaso sanguíneo, a hipótese nula será \(\mu\le0\), e a hipótese alternativa será \(\mu > 0\) , ou seja, a hipótese nula será rejeitada somente se a variação média do diâmetro do vaso for maior que o valor crítico, determinado a partir do nível de significância (α) e da distribuição da estatística utilizada. Neste caso, o valor de p será igual à probabilidade, sob a hipótese nula, de se observar um valor da estatística utilizada no teste de hipótese acima ou igual ao valor calculado na amostra utilizada no estudo.

7.2.2 Test t (Student)

7.2.2.1 Para uma média

Utilizado para testar a afirmação sobre a média populacional ou fazer comparações entre médias de duas populações.

Voltando ao nosso exemplo de vamos analisar se o uso de nosso fertilizante melhorou mesmo nossa produtividade.

Para calcular o test t no R podemos utilizar o comando t.test() e ajustar os demais parâmetros.

t.test(x, y = NULL, alternative = c("two.sided", "less", "greater"), mu = 0,
paired = FALSE, var.equal = FALSE, conf.level = 0.95, ...)

set.seed(1234)
exper<-runif(25, min = 4200, max = 4800)
exper

##  [1] 4268.222 4573.380 4565.565 4574.028 4716.549 4584.186 4205.697 4339.530
##  [9] 4599.650 4508.551 4616.155 4526.985 4369.640 4754.060 4375.390 4702.377
## [17] 4371.734 4360.092 4312.034 4339.336 4389.967 4381.616 4295.428 4223.998
## [25] 4331.280

options(scipen = 999)
t.test(exper, mu=4350, alternative="greater",conf.level = 0.95)

## 
##  One Sample t-test
## 
## data:  exper
## t = 3.1853, df = 24, p-value = 0.00199
## alternative hypothesis: true mean is greater than 4350
## 95 percent confidence interval:
##  4396.944      Inf
## sample estimates:
## mean of x 
##  4451.418

Agora basta interpretar o resultado.
Para saber se \(H_0\) foi rejeitado ou não, apenas verifique o valor de p-value e estipule um nível de sgnificância.
Neste exemplo o nível de significância (\(\alpha\)) foi 5%, então \(H_0\) seria rejeitada, uma vez que p-value foi menor que 0.05.

Neste caso observamos que a média do experimento é oriunda de uma população com média estatisticamente maior que 4350 kg ha com nível de significância de 5%. Ou seja, a utilização de fertilizante aumentou nossa produtividade de milho.

Com o argumento alternative="greater" fizemos um teste unilateral para saber se houve aumento da produtividade. Podemos variar este argumento com less para sber se foi menor ou two.sided para um teste bilateral.

options(scipen = 999)
t.test(exper,mu=4350, alternative="two.sided", conf.level = 0.95)

## 
##  One Sample t-test
## 
## data:  exper
## t = 3.1853, df = 24, p-value = 0.00398
## alternative hypothesis: true mean is not equal to 4350
## 95 percent confidence interval:
##  4385.704 4517.132
## sample estimates:
## mean of x 
##  4451.418

Para facilitar a visualização podemos utilziar o pacote webrque gerar uma gráfico destacando a região de rejeição de nossa hipótese e a posição do p-value.

a região rosa é a região de rejeição de \(H_0\) e ponto azul o t calculado.

#if (!require("webr")) install.packages("webr")
library(webr)

## Registered S3 method overwritten by 'psych':
##   method         from  
##   plot.residuals rmutil

plot(t.test(exper, mu=4350, alternative="greater", conf.level = 0.95))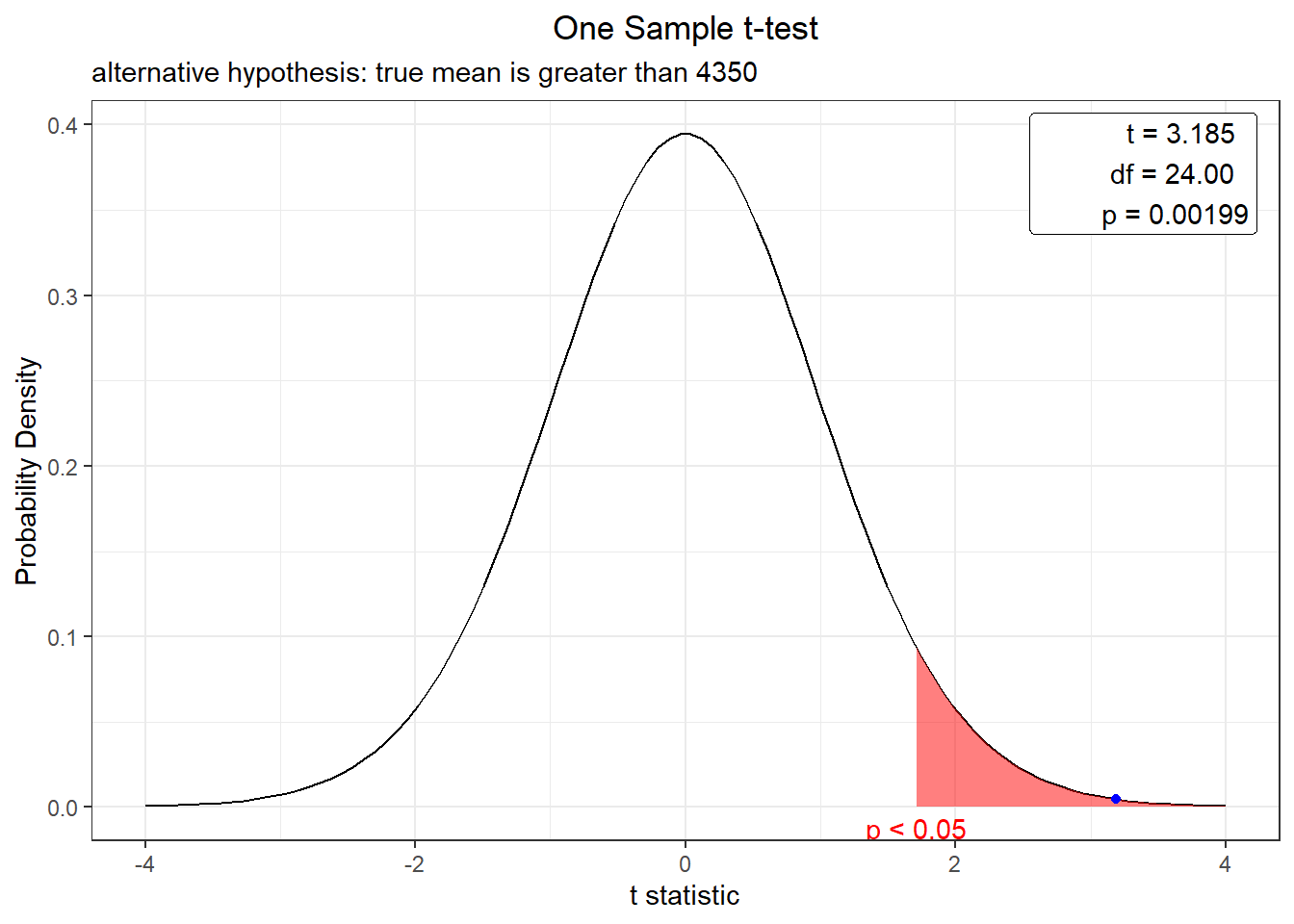

plot(t.test(exper, mu=4350, alternative="less", conf.level = 0.95))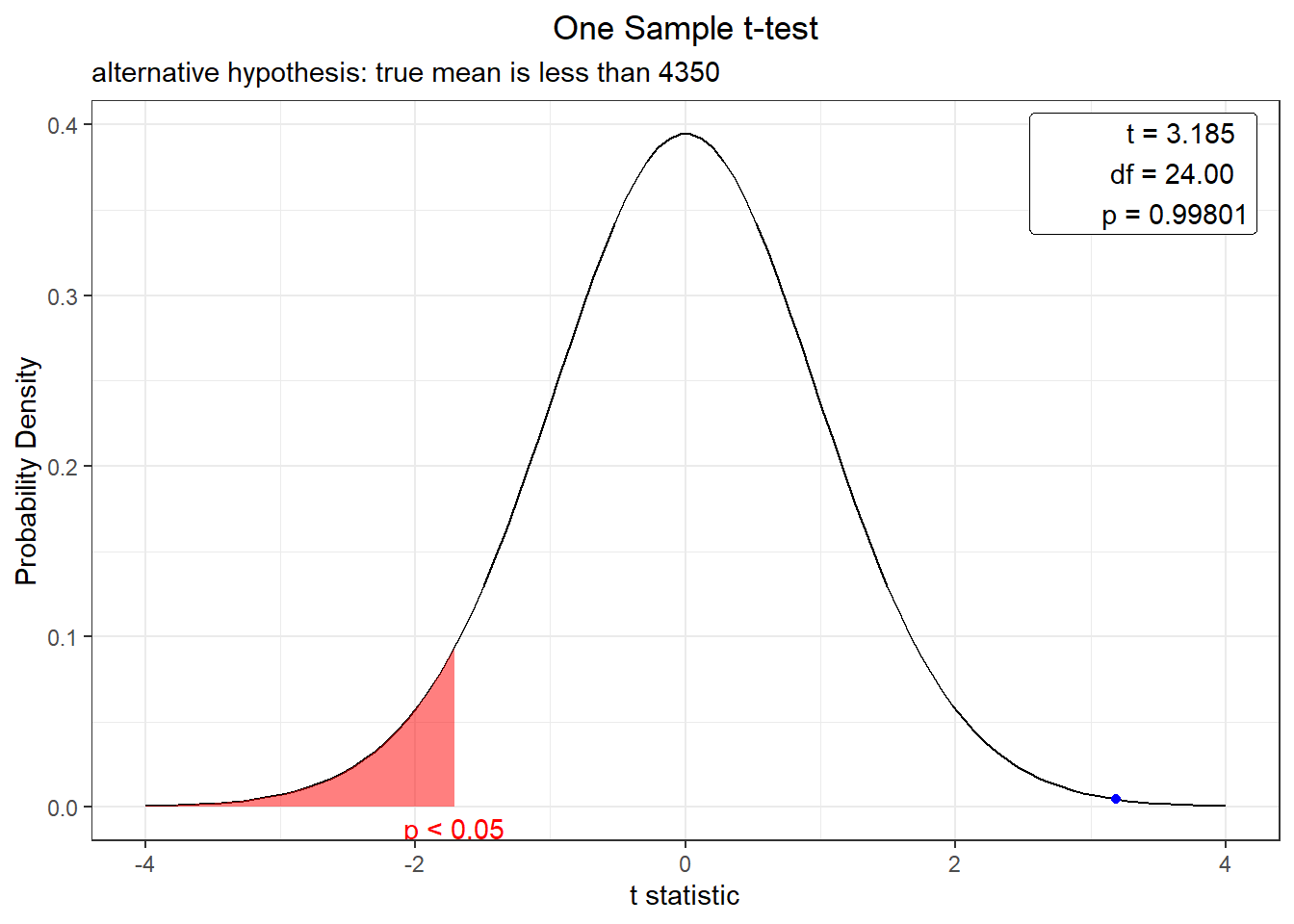

plot(t.test(exper, mu=4350, alternative="two.sided", conf.level = 0.95))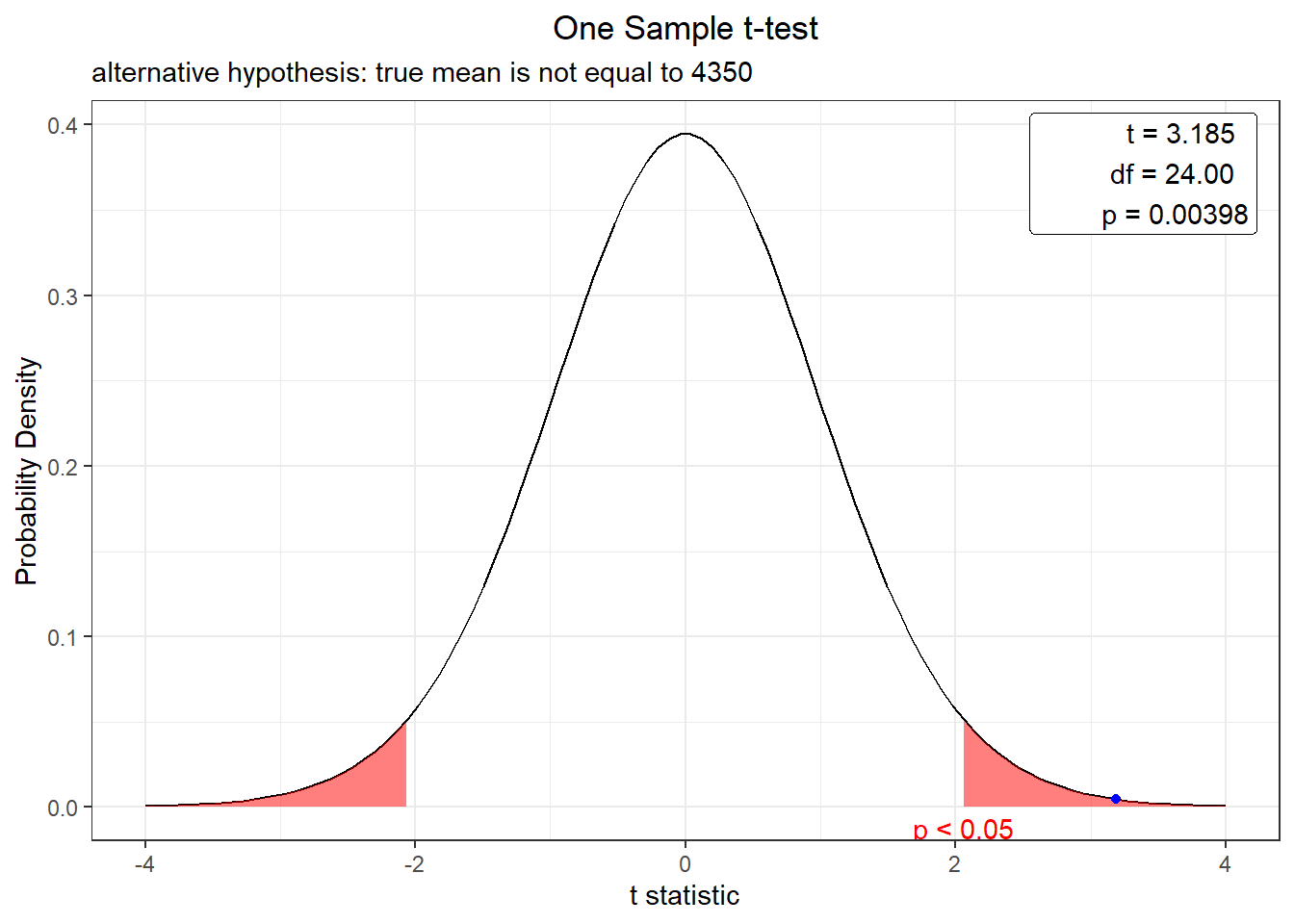

7.2.2.2 Duas amostras independentes

Vamos considerar agora que um novo experimento foi feito com um novo fertilizante lançado no mercado. Gostaríamos de saber se apresentam comprtamento semelhante, pois quero comprar o mais barato e, se forem iguais, fico com o mais barato.
Vamos considerá-las com variâncias não homogêneas var.equal = F.

set.seed(1234)
exper2<-runif(25, min = 3500, max = 5200)
exper2

##  [1] 3693.296 4557.909 4535.767 4559.745 4963.556 4588.528 3516.143 3895.336
##  [9] 4632.342 4374.227 4679.105 4426.457 3980.647 5069.837 3996.937 4923.403
## [17] 3986.580 3953.595 3817.429 3894.784 4038.241 4014.579 3770.378 3567.993
## [25] 3871.959

plot(t.test(exper,exper2,var.equal = F, alternative="less", conf.level = 0.95))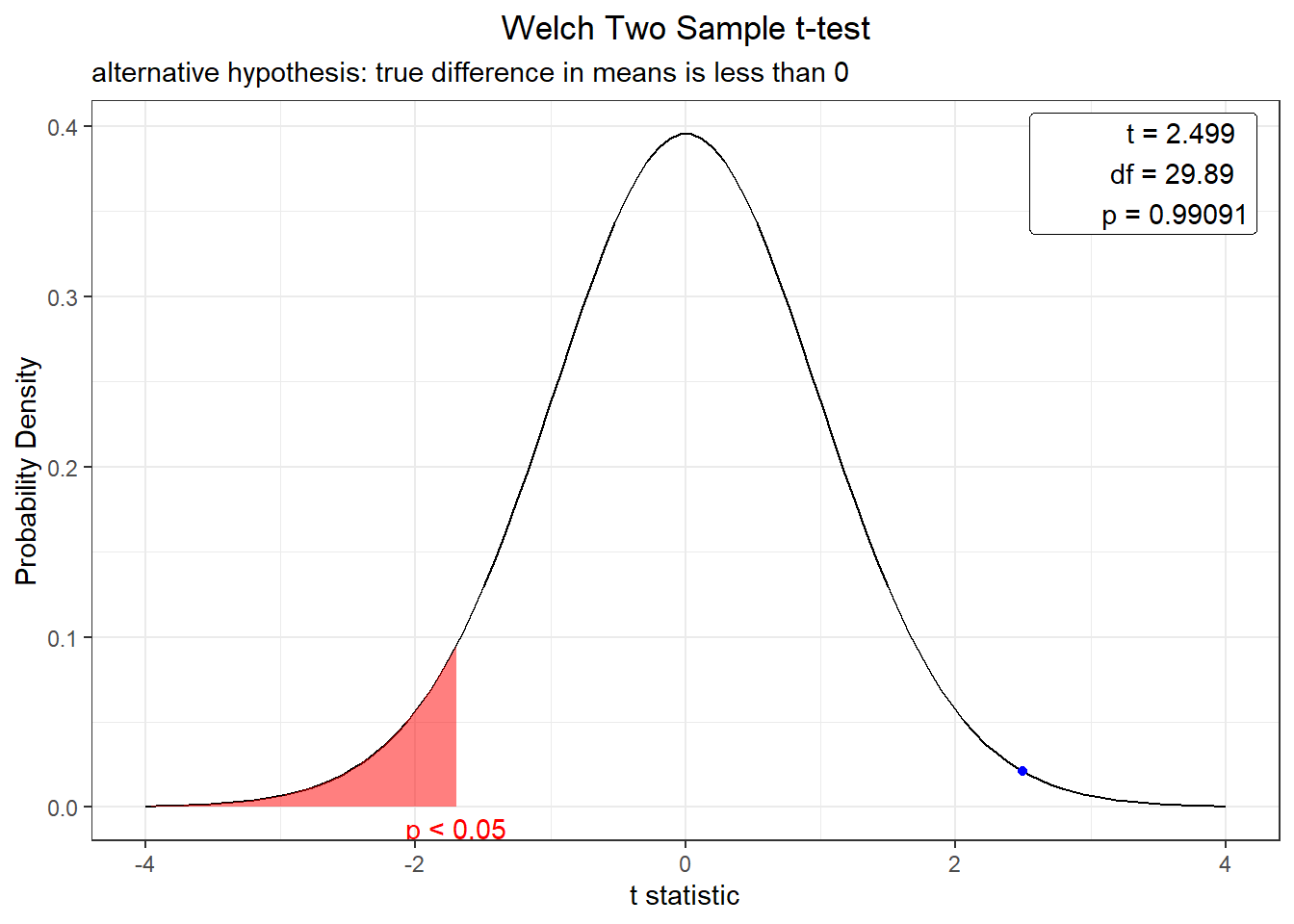

plot(t.test(exper,exper2,var.equal = F, alternative="greater", conf.level = 0.95))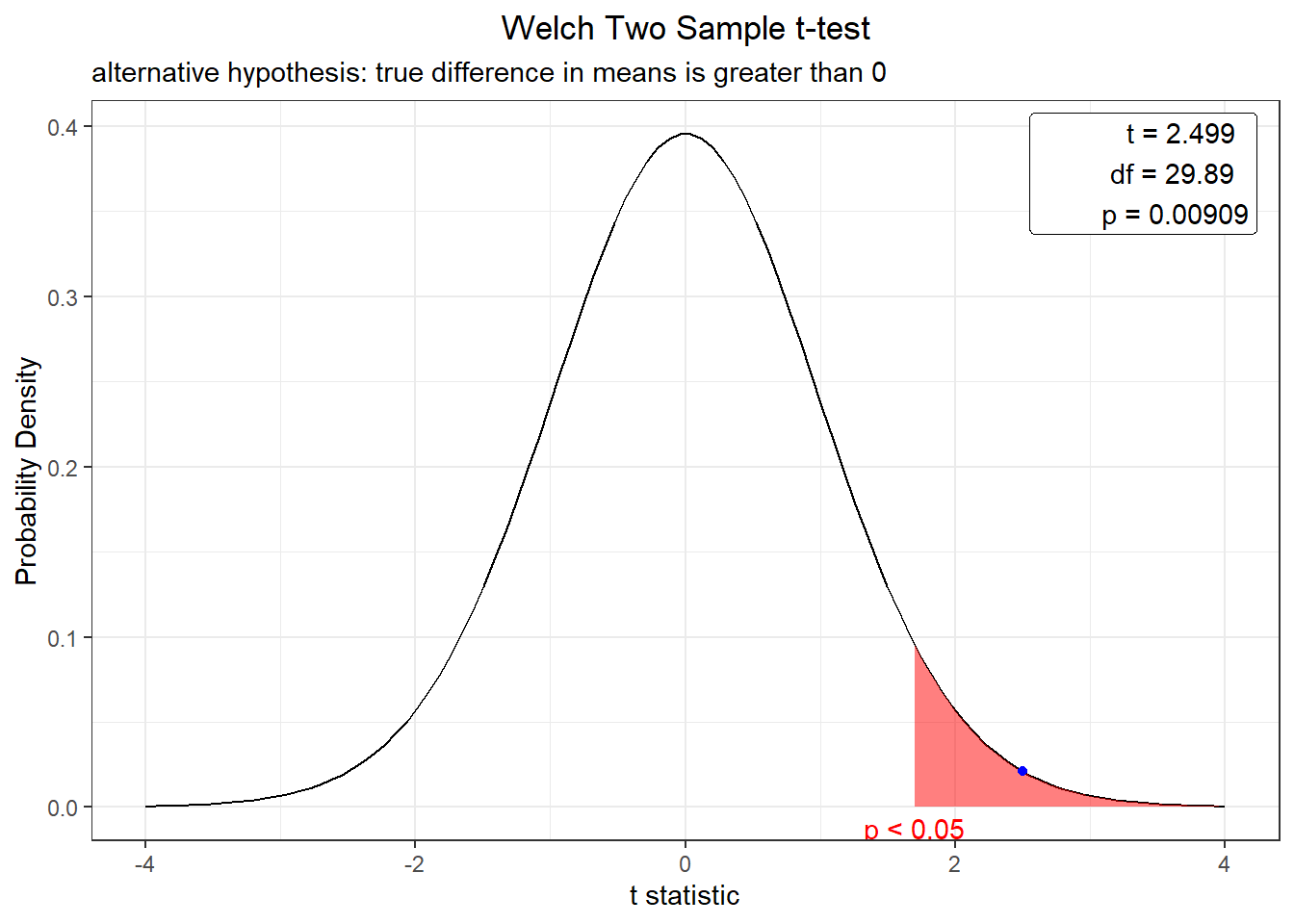

plot(t.test(exper,exper2,var.equal = F, alternative="two.sided", conf.level = 0.95))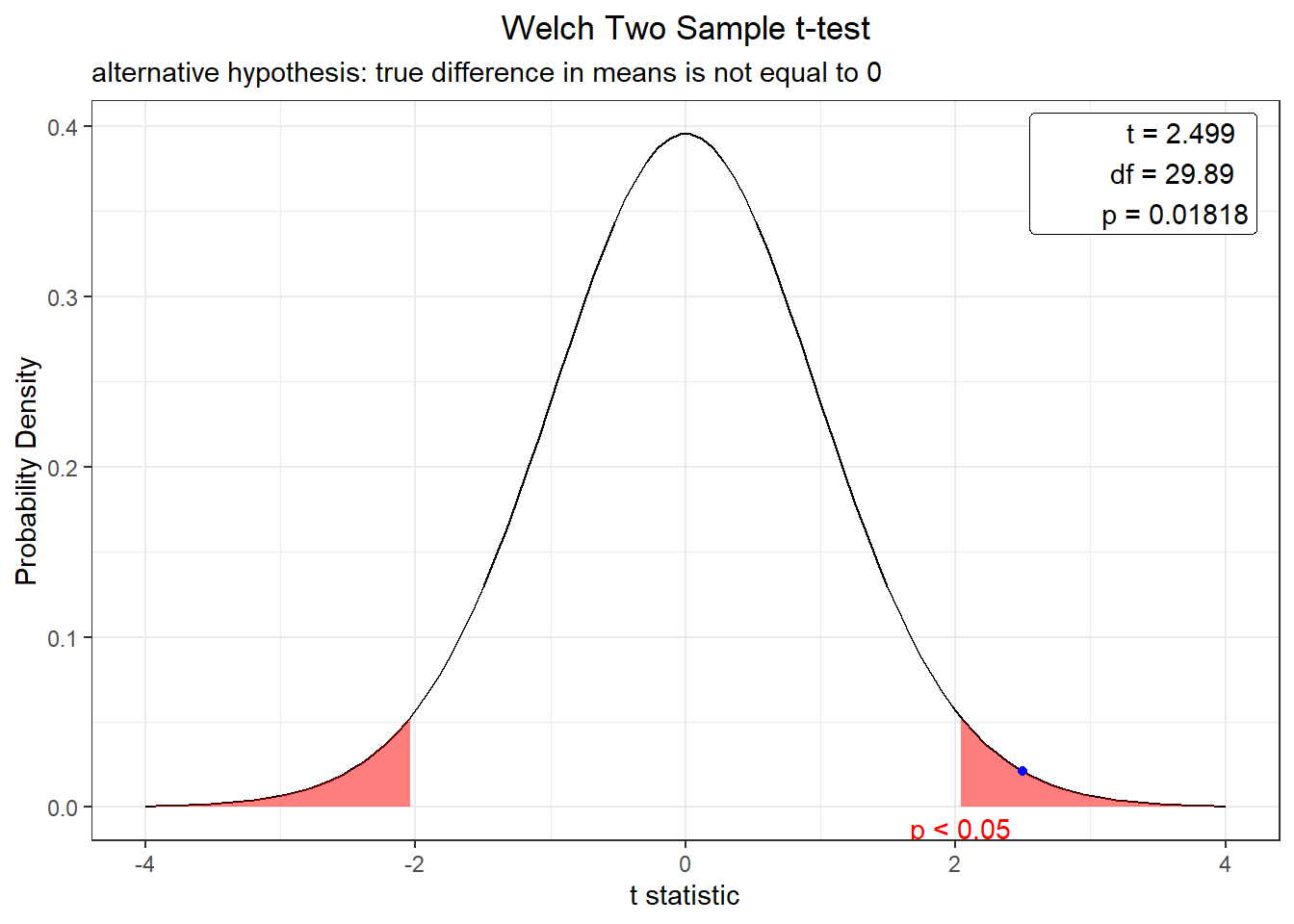

Rejeitamos as hipótese nula apenas no primeiro caso, pois p-value foi maior que *0.05. Nos demais não rejeitamos a hipótese nula assumimos então que a produtividade com os 2 fertilizantes são diferentes, estatisticamente , a 5% de significância.

7.2.2.3 Para duas amostras dependentes

Quando temos pares de amostras (X e Y) coletadas dos mesmos indivíduos, temos um teste pareado. Neste caso basta acrescentar o argumento paired=T.

plot(t.test(exper,exper2,var.equal = F,paired=T, alternative="less", conf.level = 0.95))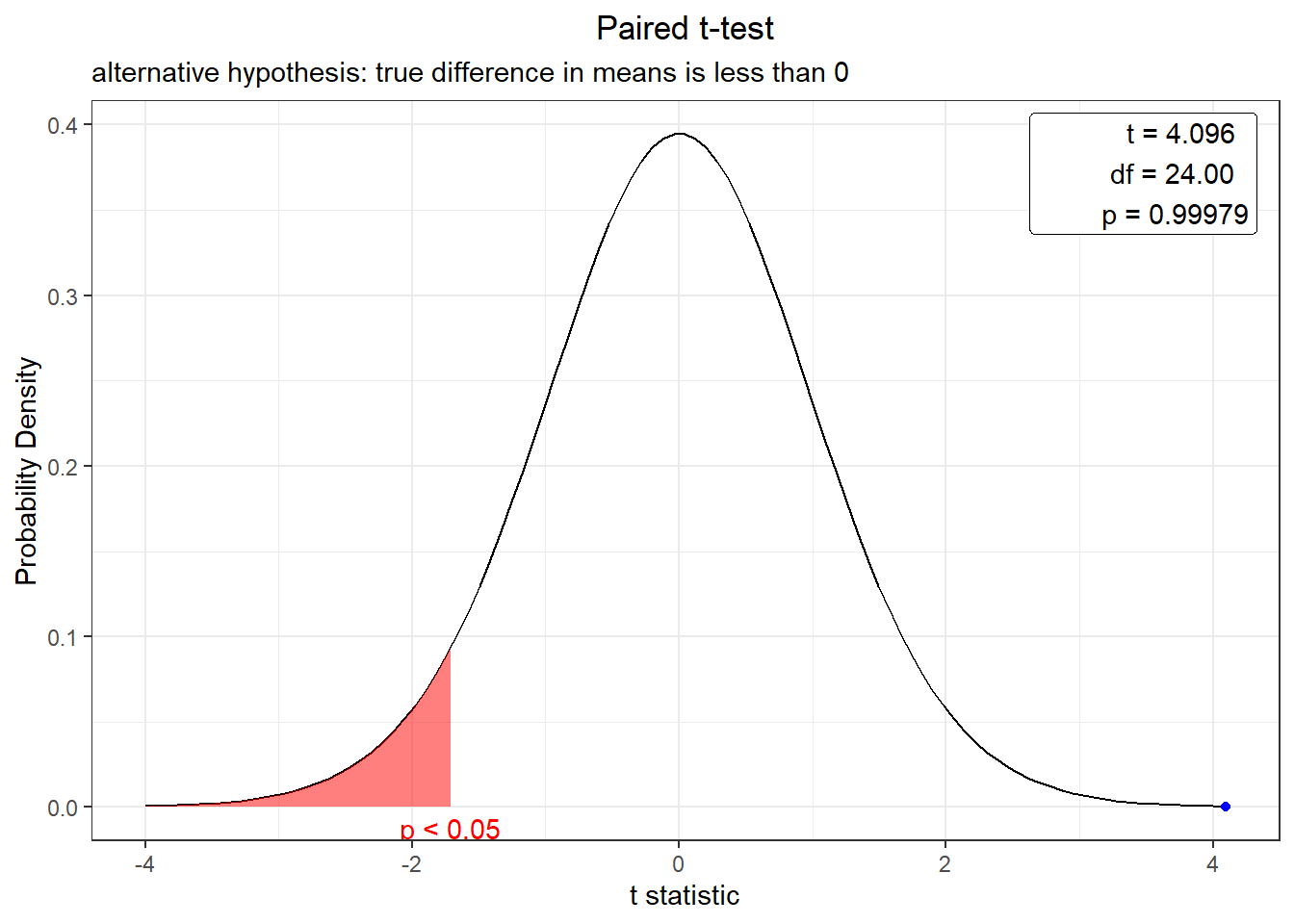

plot(t.test(exper,exper2,var.equal = F,paired=T, alternative="greater", conf.level = 0.95))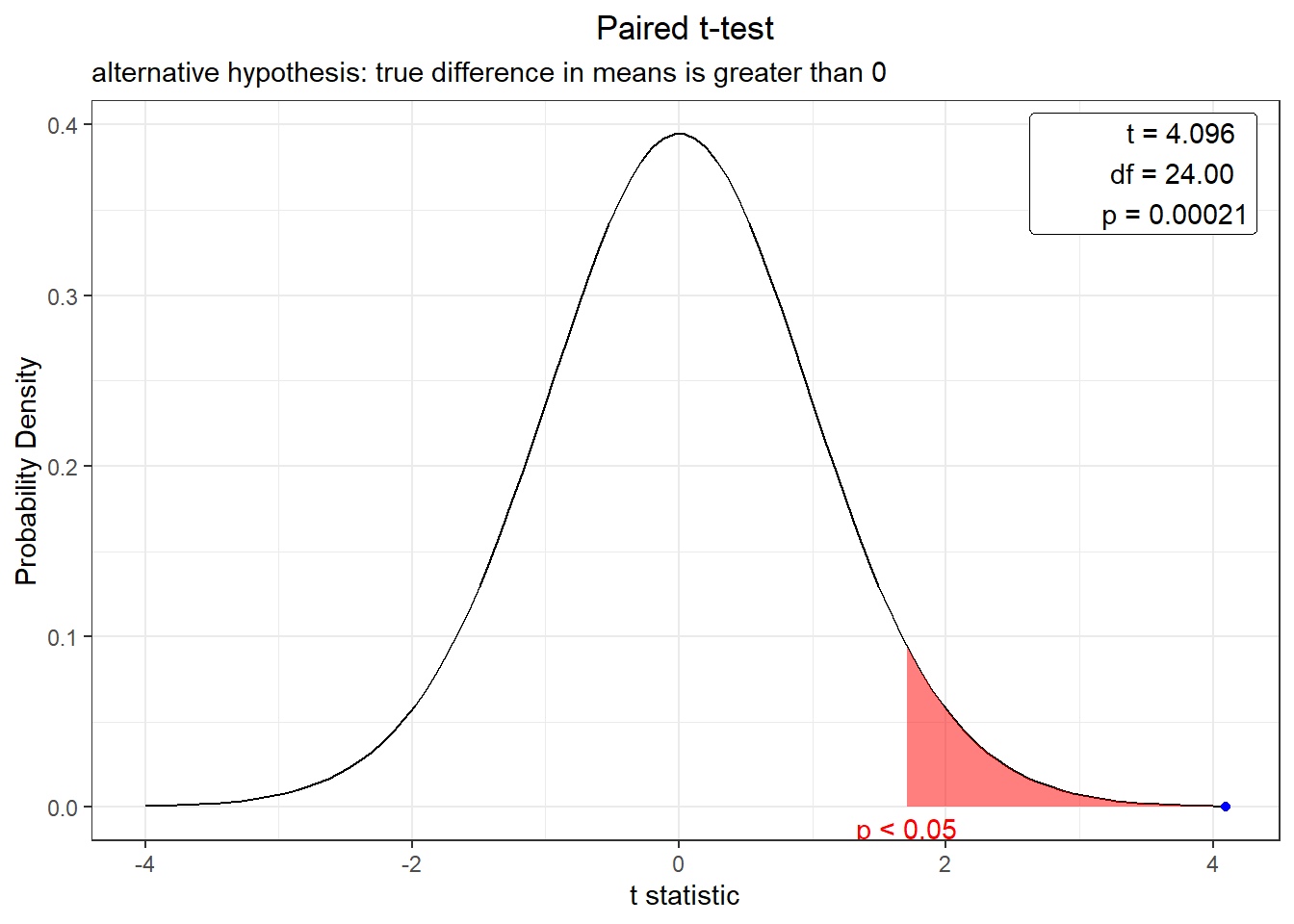

plot(t.test(exper,exper2,var.equal = F,paired=T, alternative="two.sided", conf.level = 0.95))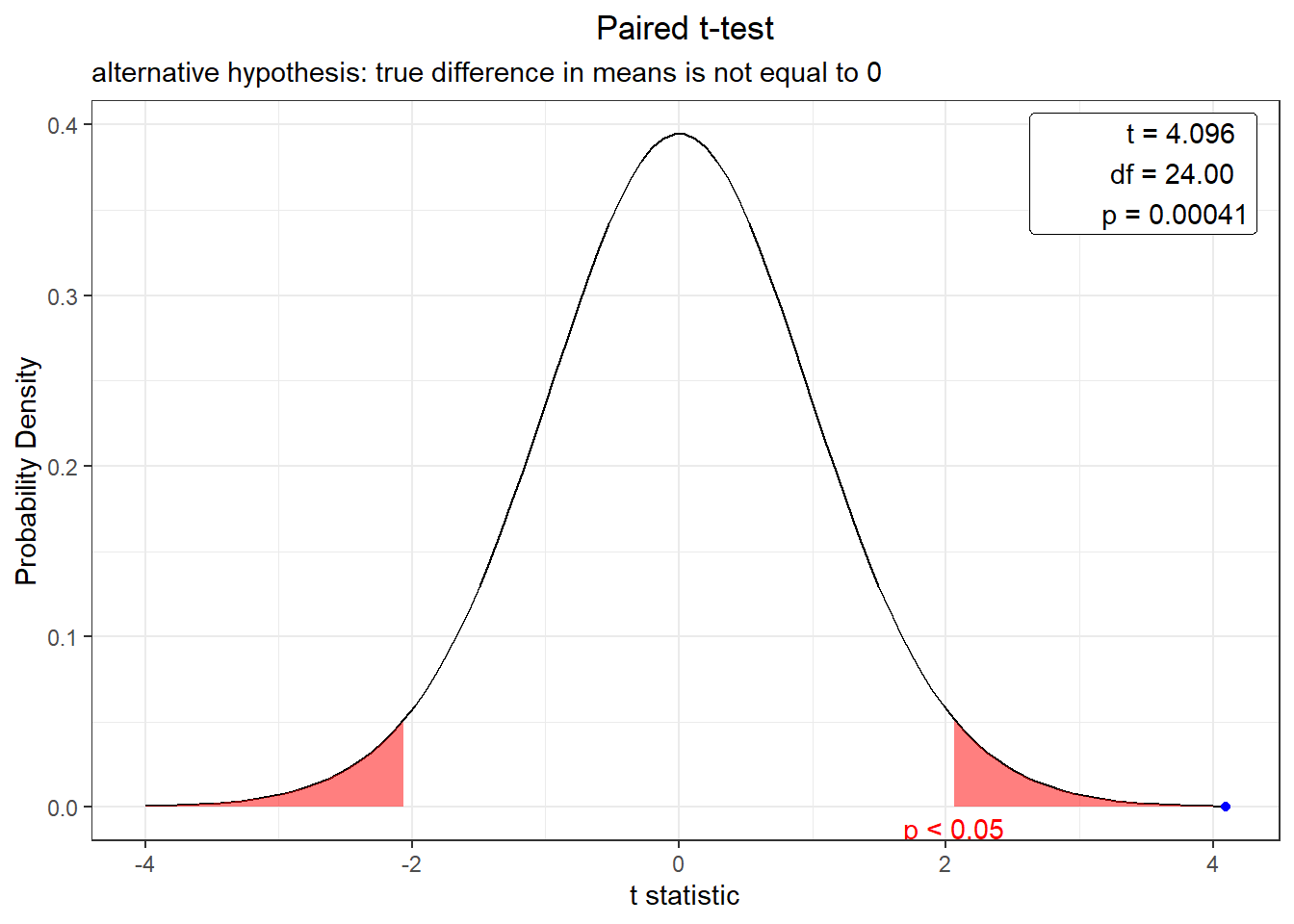

7.2.3 Teste F

Métodos utilizado verificar se as variâncias de amostras normalmente distribuídas são homogêneas.

\(H_0: \sigma^2_A = \sigma^2_B\)

\(H_1: \sigma^2_A > \sigma^2_B\)

exper

##  [1] 4268.222 4573.380 4565.565 4574.028 4716.549 4584.186 4205.697 4339.530
##  [9] 4599.650 4508.551 4616.155 4526.985 4369.640 4754.060 4375.390 4702.377
## [17] 4371.734 4360.092 4312.034 4339.336 4389.967 4381.616 4295.428 4223.998
## [25] 4331.280

exper2

##  [1] 3693.296 4557.909 4535.767 4559.745 4963.556 4588.528 3516.143 3895.336
##  [9] 4632.342 4374.227 4679.105 4426.457 3980.647 5069.837 3996.937 4923.403
## [17] 3986.580 3953.595 3817.429 3894.784 4038.241 4014.579 3770.378 3567.993
## [25] 3871.959

n1<-length(exper)
n2<-length(exper2)

vm1<-var(exper)
vm2<-var(exper2) 

fcal<-(vm1/vm2)
fcal

## [1] 0.1245675

pval<-pf(fcal, n1-1, n2-1, lower=F)
pval

## [1] 0.9999986

Nest caso nosso nível de significância é 5% e o p-value foi 0.9999986. \(H_0\) não é rejeitada, pois o p-value foi maior que que o nível de significância. Assim, a variância da produtividade em A não é estatisticamente maior que da produtividade em B.

Acima fizemos um passo a passo, mas existe uma forma mais fácil de conduzir esta análise utilizando o comando var.test().

x1<-var.test(exper, exper2, alternative="greater")
x1;plot(x1)

## 
##  F test to compare two variances
## 
## data:  exper and exper2
## F = 0.12457, num df = 24, denom df = 24, p-value = 1
## alternative hypothesis: true ratio of variances is greater than 1
## 95 percent confidence interval:
##  0.06279363        Inf
## sample estimates:
## ratio of variances 
##          0.1245675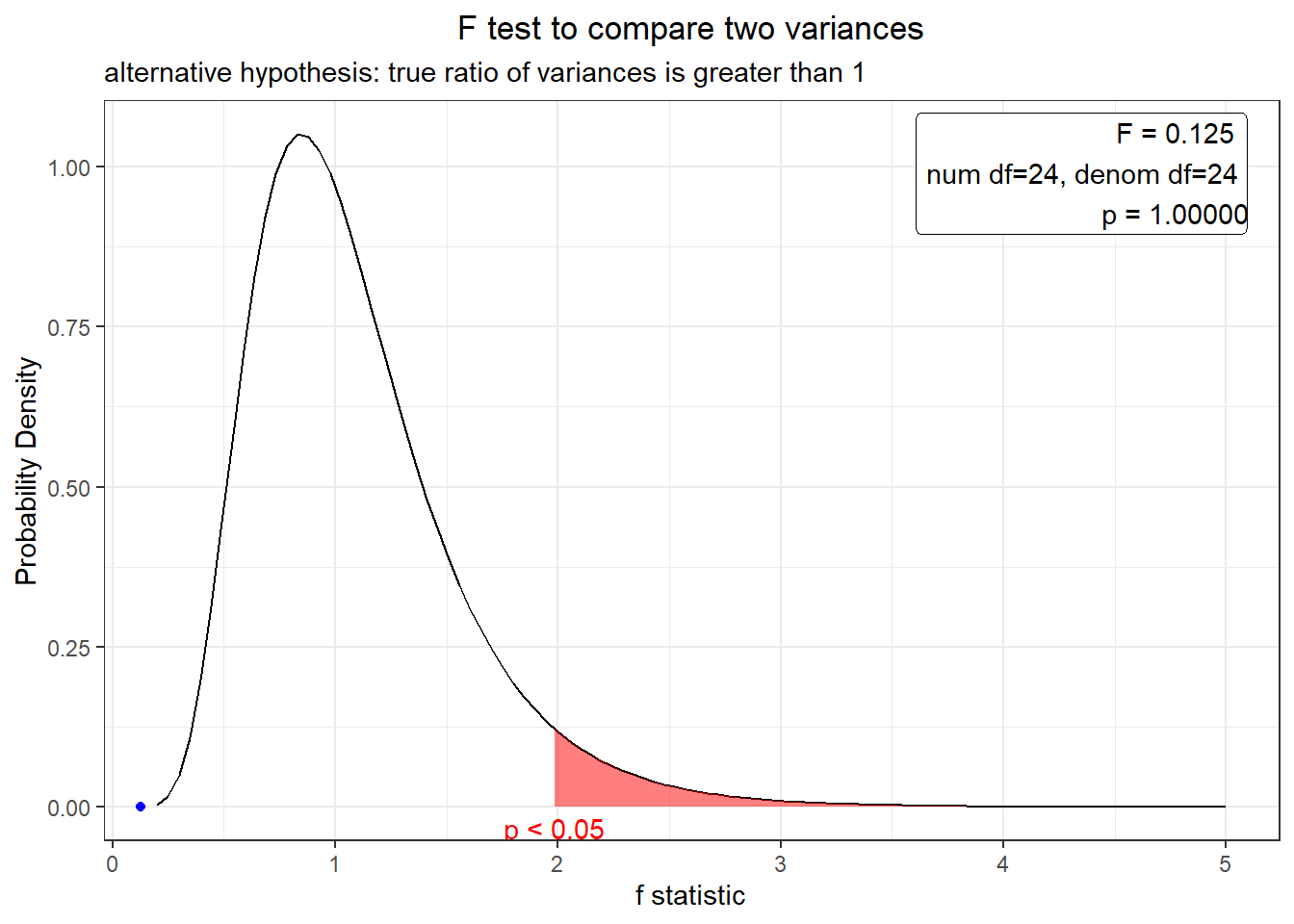

x2<-var.test(exper, exper2, alternative="less")
x2;plot(x2)

## 
##  F test to compare two variances
## 
## data:  exper and exper2
## F = 0.12457, num df = 24, denom df = 24, p-value = 0.000001415
## alternative hypothesis: true ratio of variances is less than 1
## 95 percent confidence interval:
##  0.0000000 0.2471119
## sample estimates:
## ratio of variances 
##          0.1245675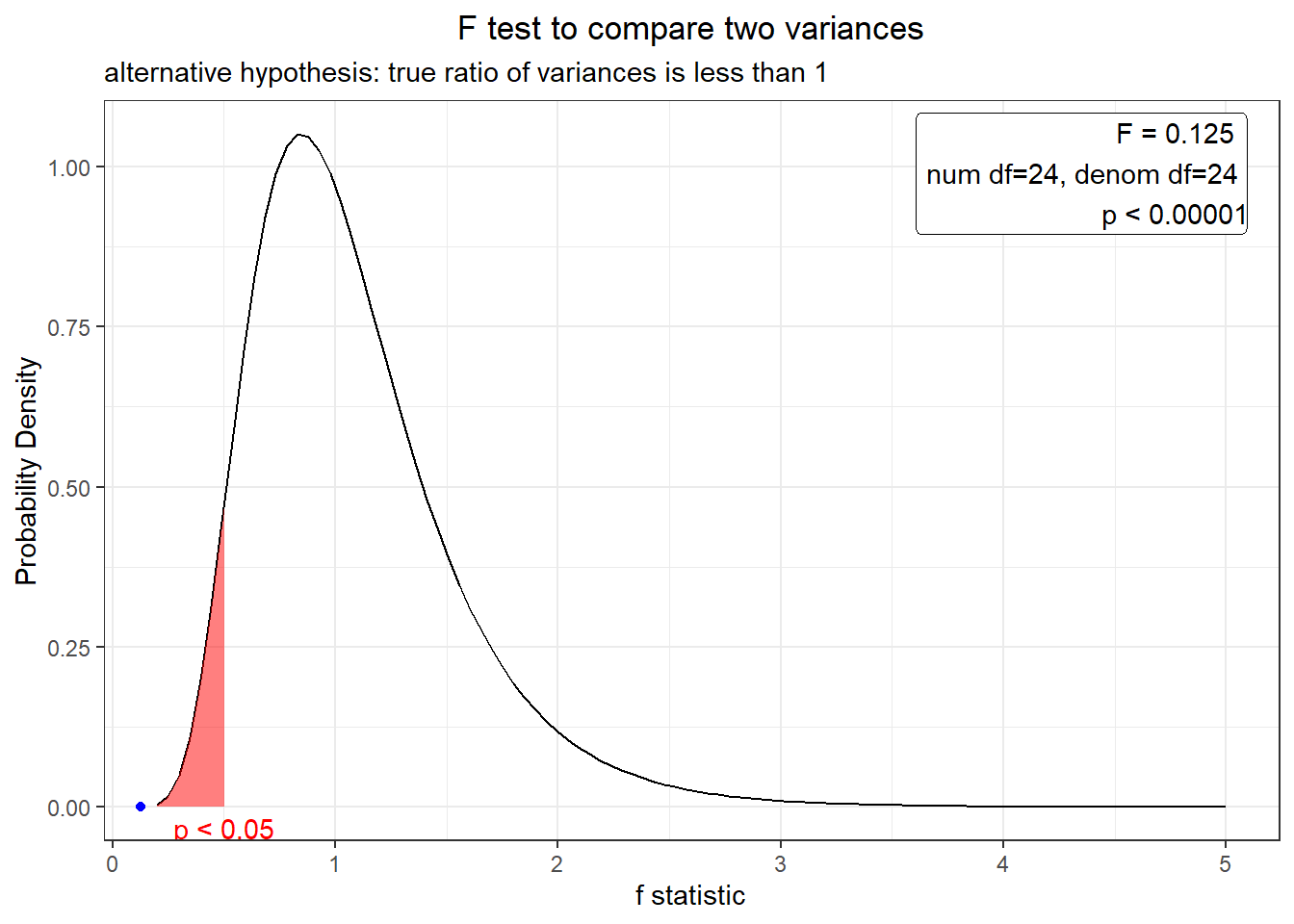

x3<-var.test(exper, exper2, alternative="two.sided")
x3;plot(x3)

## 
##  F test to compare two variances
## 
## data:  exper and exper2
## F = 0.12457, num df = 24, denom df = 24, p-value = 0.000002829
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.05489302 0.28267814
## sample estimates:
## ratio of variances 
##          0.1245675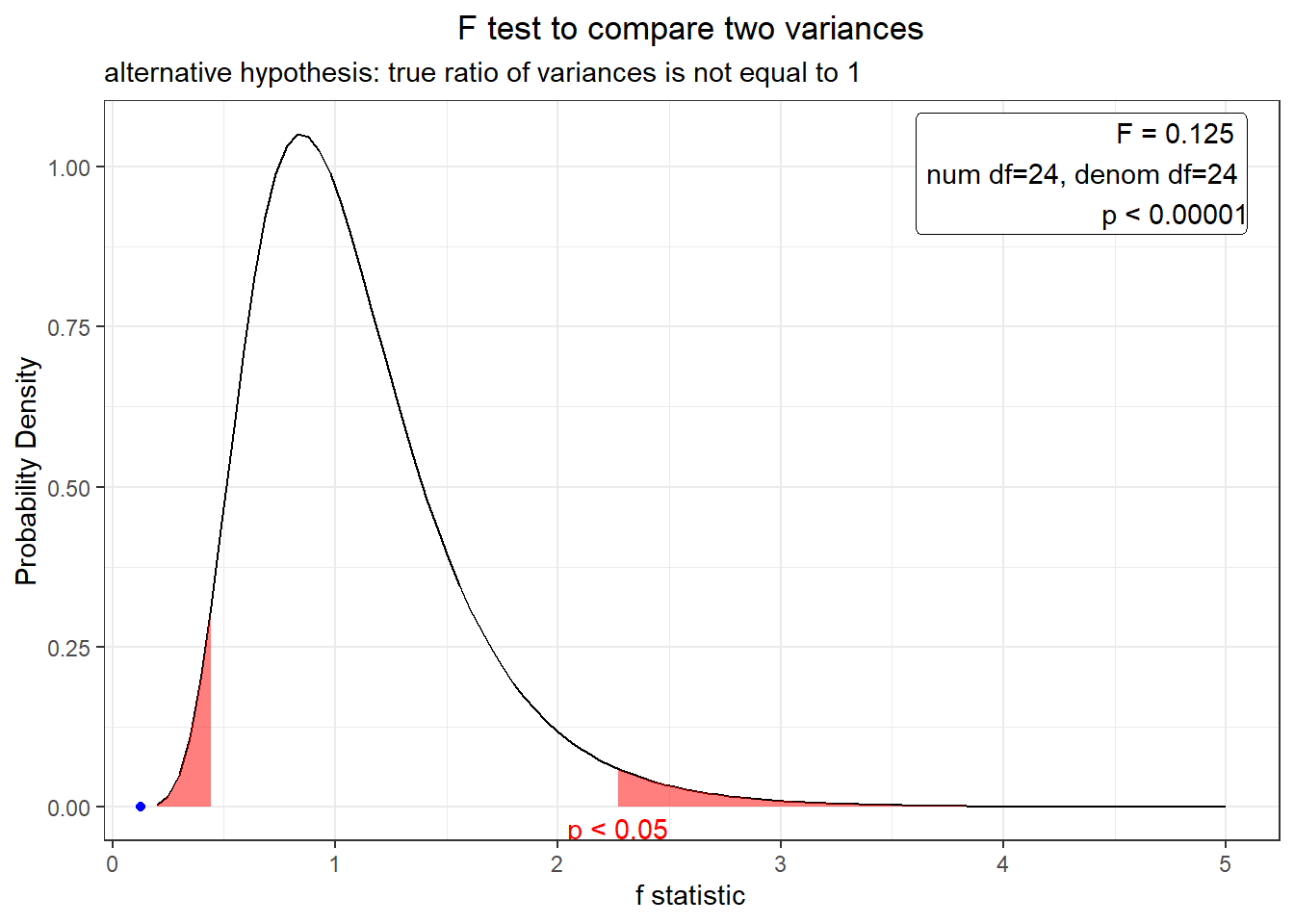

7.2.3.1 Kolmogorov-Smirnov

O teste de Kolmogorov-Smirnov é utilizado para sabermos se um banco de dados segue alguma distribuição específica (Mello and Peternelli (2013)).

No R o teste Kolmogorov-Smirnov para testar uma ditribuição pode ser acessado pelo comando ks.test(x,"pdistribuição", mean(), sd()).

ks.test(exper,"pnorm",mean(exper),sd(exper)) 

## 
##  Exact one-sample Kolmogorov-Smirnov test
## 
## data:  exper
## D = 0.21025, p-value = 0.1899
## alternative hypothesis: two-sided

p-value não é menor que 0.05, desta forma podemos assumir que os dado exper não são significativamente diferentes de distribuição normal.

7.2.3.2 Teste de Shapiro

Outro teste para normalidade de dados é o teste de shapiro.
No R pode ser implementado utilizando shapiro.test()

shapiro.test(exper)

## 
##  Shapiro-Wilk normality test
## 
## data:  exper
## W = 0.93315, p-value = 0.1028

shapiro.test(exper2)

## 
##  Shapiro-Wilk normality test
## 
## data:  exper2
## W = 0.93315, p-value = 0.1028

The p-value de exper e exper2 são {r shapiro.test(exper)} e {r shapiro.test(exper2)}, respectivamente. Ambos são maiores que 0.05, desta forma concluimos que a distribuição de ambos experiemntos não são significativamente diferentes de uma distribuição normal.

Podemos tentar compreender melhor as distribuições utilizando gráficos.

Se a dispersão dos pontos segue um padrão aproximado de uma linha entyendemos assim que os dados são normalmente distribuídos.

qqnorm(exper);qqline(exper)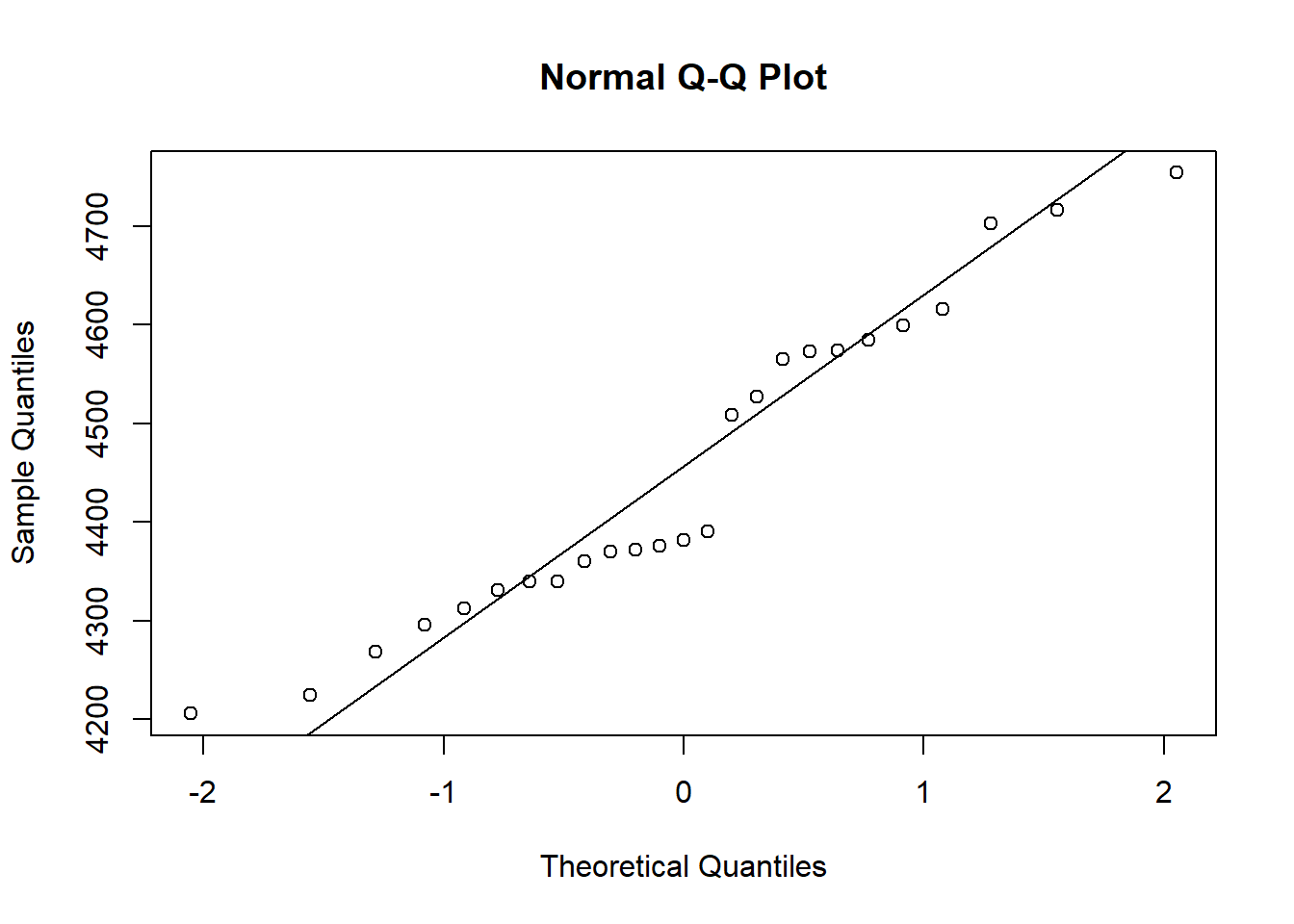

qqnorm(exper2);qqline(exper2)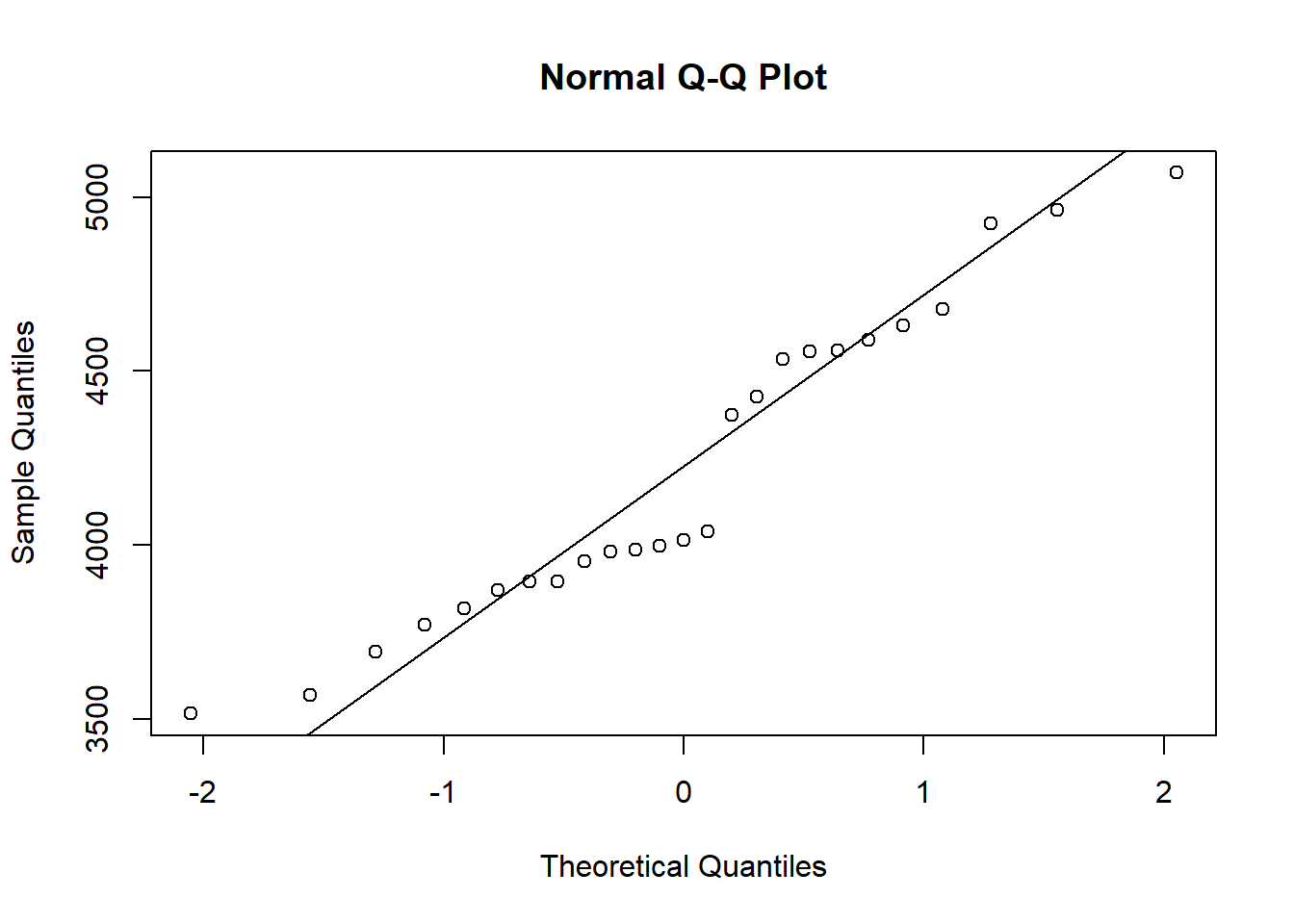

Existe uma infinidade de testes para serem conduzidos para explorar seus dados. Por isso procure um bom livro de estatística para compreender qual o melhor teste para seu caso.

Para implementação destes teste no R, vimos que não é tão complexo e encontramos facilmente material de suporte na internet.

Caso queiram explorar os testes conduzidos no R digitem no console apropos("test") que lista tudo que tenha a palavra test ou help.search("test") que listará os comandos encontrados nos pacotes instalados.

apropos("test")

##  [1] ".valueClassTest"         "ansari.test"            
##  [3] "associationTest"         "bartlett.test"          
##  [5] "binom.test"              "binom.test"             
##  [7] "Box.test"                "chisq.test"             
##  [9] "clamtest"                "cor.test"               
## [11] "cor.test"                "cor_test"               
## [13] "cox.stuart.test"         "fieller.MOStest"        
## [15] "file_test"               "fisher.test"            
## [17] "fligner.test"            "flow_test"              
## [19] "friedman.test"           "goodnessOfFitTest"      
## [21] "independentSamplesTTest" "kruskal.test"           
## [23] "ks.test"                 "mantelhaen.test"        
## [25] "mauchly.test"            "mcnemar.test"           
## [27] "mood.test"               "MOStest"                
## [29] "oneSampleTTest"          "oneway.test"            
## [31] "ordiareatest"            "pairedSamplesTTest"     
## [33] "pairwise.prop.test"      "pairwise.t.test"        
## [35] "pairwise.wilcox.test"    "permutest"              
## [37] "poisson.test"            "power.anova.test"       
## [39] "power.prop.test"         "power.t.test"           
## [41] "PP.test"                 "prop.test"              
## [43] "prop.test"               "prop.trend.test"        
## [45] "prop_test"               "protest"                
## [47] "quade.test"              "runs.test"              
## [49] "shapiro.test"            "stat_anova_test"        
## [51] "stat_friedman_test"      "stat_kruskal_test"      
## [53] "stat_welch_anova_test"   "t.test"                 
## [55] "t.test"                  "t_test"                 
## [57] "testInheritedMethods"    "testVirtual"            
## [59] "theme_test"              "var.test"               
## [61] "wilcox.test"             "xchisq.test"

help.search("test")

Para mais detalhes sobre os testes e sobre sua utilização no R podem acessar o material online como Pires et al. (2018) e Freire (2021a).

Outras fontes muito interessantes para implemenação de estatíticas no R com exemplos são Yamamoto (2020), Midway (2020) e Kabacoff (2015).

References

Freire, S. M. 2021a. Bios Estatística Básica. 1st ed. Creative Commons. http://www.lampada.uerj.br/arquivosdb/_book/bioestatisticaBasica.html.

Kabacoff, Robert I. 2015. R in Action. Second. Manning. http://www.worldcat.org/isbn/9781617291388.

Levin, J., J. A. Fox, and D. R. Forde. 2012. Estatistica Aplicada a Ciencias Humanas. Pearson.

Mello, M. P., and L. A. Peternelli. 2013. Conhecendo o r: Uma Visão Mais Que Estatística. First. Editora UFV.

Midway, S. 2020. Data Analysis in r. bookdown. https://bookdown.org/steve_midway/DAR/.

Navarro, D. 2013. Learning Statistics with r: A Tutorial for Psychology Students and Other Beginners (version 0.6.1). bookdown. https://bookdown.org/ekothe/navarro26/preface.html.

Pires, M. C., M. B. Castro, Z. V Lieber, T. P. Menezes, and R. Y. da S. Aoki. 2018. Estatística Não Paramétrica Básica No Software r: Uma Abordagem Por Resolução de Problemas. UFMG. http://www.est.ufmg.br/portal/arquivos/rts/RTE_02_2018.pdf.

Yamamoto, J. K. 2020. Estatística, Análise e Interpolação de Dados Geoespaciais. 1st ed. São Paulo: Gráfica Paulos.